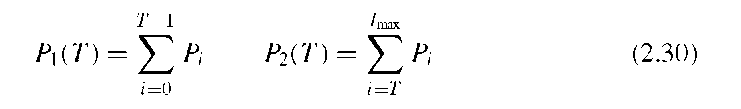The purpose of segmentation is to separate one or more regions of interest in an image from regions that do not contain relevant information. Regions that do not contain relevant information are called background. Depending on the image, segmentation can be a very complex process, and a comprehensive overview of the most relevant segmentation techniques could fill an entire topic. For our purposes in this topic, an overview of simple intensity-based techniques is given. The underlying assumption is that pixels belonging to the features of interest occupy a different value range than that of background pixels. Without loss of generality, all examples in this topic assume that background pixels have lower values than feature pixels.
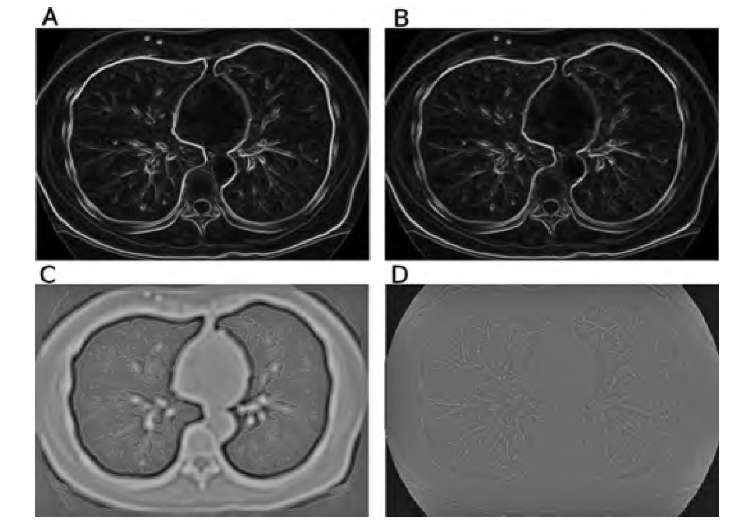
FIGURE 2.8 Demonstration of some edge detection operators. The original image is the CT slice in Figure 2.7A. Images A and B show the results of the Sobel and compass edge detectors with color-coded edge directions. Whereas the edge magnitude is very similar, the discrete nature of the edge directions in the compass operator becomes clearly visible. In image C the LoG operator with ct = 3.0 was applied, and zero crossings (edge locations) are marked in red. An apparent double edge appears at the steepest edges. Image D shows a color-coded version of the Frei-Chen operator. Red hues indicate high values (low projection angles) in edge space, with some similarity to the Sobel and compass operators. Blue-green hues indicate high values in line space, most prominent in the vascular structure and the thin traces of the ribs.
If we assume further that the distribution of feature pixels and background pixels is approximately Gaussian, a characteristic intensity distribution with two peaks in the histogram emerges (Figure 2.9). Such a distribution is called bimodal because there are two mode values: one for the background and one for the feature. Intensities are normally spread around the modal values because of the additive noise and intensity inhomogeneities of the features. The simplest approach for segmentation would be the selection of a suitable intensity threshold, as indicated in Figure 2.9. All pixels with a value higher than the threshold value are classified as feature pixels, and all pixels with a lower value are classified as background pixels. Most commonly, a new image is created by using
where I(x,y) are the original image pixels and IT(x,y) is the thresholded image. Since IT contains only two values (1 for foreground pixels and 0 for background pixels), it is called a binary image. It can serve as a mask because each location (x,y) of the original image has a value of 1 in the mask if this is a feature pixel.
FIGURE 2.9 Bimodal histogram. In this example, background pixels are generally darker than feature pixels. However, the intensities spread because of noise and intensity inhomo-geneities. Intensity-based separation can be carried out with a suitable threshold, but some pixels are misclassified.
In many cases, some feature pixels will have intensity values below the threshold value, and some background pixels will lie above the threshold value because of image inhomogeneities and additive noise. With pure intensity-based thresholding, these pixels cannot be classified correctly (misclassified pixels in Figure 2.9). Two questions need to be answered. First, is there any way to determine the optimum threshold value automatically, and second, what steps can be taken to decrease the number of misclassified pixels?
Automated Threshold-Finding Methods
A number of methods exist to find the valley between the two modal peaks in a histogram, and three representative examples are introduced: the isodata method20 (also called the iterative thresholding method), Otsu’s method,17 and the entropy maximization method.13 Iterative thresholding is arguably the easiest method to implement, and Otsu’s method is one of the most widely used methods. Both methods, and other methods not described here, work under the assumption of a bimodal histogram with a well-defined valley; in practice, different thresholding methods find very similar values in ideal cases but may vary when the assumptions are not met. All methods will provide a threshold value when acting on a single-modal histogram, but the resulting threshold value may not be useful.
For iterative thresholding, an initial threshold Tk = 0 must be specified, and a good choice is the mean gray value of the image. Ridler and Calvard20 originally proposed using rectangular regions at the four corners of the image as background and the rest of the image as foreground, but the final threshold is independent of the initial choice, and almost any convenient initial threshold may be used. For the iterative process, the image is then partitioned into a set of pixels S1 with values below the threshold Tk of the current iteration and a set of pixels S2 with values above or equal to Tk. Next, the mean gray values and of the pixel sets S1 and S2 are computed, and a new threshold, Tk +1, is computed as + ^2)/2. The partitioning is now repeated with the new threshold value until the iteration converges with |Tk – Tk+11 < €. The convergence criterion € may be a suitable small value: for example, 0.5 for integer-valued images.
Otsu’s method assumes a Gaussian distribution of the image values around both modes, and the goal of Otsu’s strategy is to maximize the between-group variance ctB, that is, to choose a threshold that maximizes the variance between feature and background pixels. Otsu showed that this maximization also minimizes the combined variance within feature and background classes. Let nI be the number of pixels with image value I and N the total number of pixels. The probability of image value I is then PI = hi/N. If we consider a threshold T that divides the image into the pixel sets S1 (below the threshold) and S2 (above or equal to the threshold), the cumulative probabilities P1 and P2 of the sets S1 and S2 are defined as
The first and second statistical moments are the mean values and within-class variances for the two classes S1 and S2:
Furthermore, the mean value and variance of the entire image can be obtained through the equation
With these definitions, the combined within-class variance can be computed as
All values
, and P2, and consequently,
are functions of the threshold T. Otsu proposed a threshold function i|(T) defined as
which can be used as a measure of the goodness of the threshold value T,17 and the optimum threshold can be found by performing an exhaustive search of all possible T’s for the value of T that maximizes r|(T). Since ct} is a constant, it is possible to search for a value of T that maximizes ctJ instead. Furthermore, since
, Equation (2.34) can be skipped completely and a value of T that minimizes
can be searched instead. All of these variations lead to the same value of T.
Methodically similar is a method to maximize combined entropy. Following the definitions in Equation (2.30), the entropies H1 and H2 of the background and foreground sets S1 and S2 are defined by
The optimum threshold can be found by searching exhaustively for a threshold T that maximizes the combined entropy H(T) = H1(T) + H2(T).13
The second question concerns the number of misclassified pixels (Figure 2.9). The application of noise-reduction filters has the potential to narrow the pixel distributions. Here is where Gaussian blurring comes into play, which from a purely visual perspective seems counterintuitive. The application of a median filter or center-weighted median filter to remove extreme values, followed by Gaussian blurring, is a suitable preparation for intensity-based thresholding. The background peak distribution can be narrowed by applying unsharp masking or a homomorphic highpass filter (see Section 3.2) to remove background inhomogeneities. Furthermore, intensity-based thresholding can be improved by making use of connectedness. This gives rise to techniques such as region growing and hysteresis thresholding.
Thresholding with Multiple Thresholds
In cases where a feature with intermediate image values needs to be separated from a darker background and brighter features, the histogram would show three modes. The intermediate mode can be separated with two thresholds T1 and T2, where T1 < T2. The image with the thresholded feature is then converted into a binary mask:
and the between-class variance
can be defined by
With multiple thresholds, computational efficiency is reduced, as a (n – 1)-dimensional space needs to be searched exhaustively for the combination of thresholds that minimizes ct^. Furthermore, the search for multiple thresholds becomes less stable with increasing n and less credible thresholds. For the most common cases, n = 2 and n = 3, the method remains robust.
Region Growing
Normally, a feature is characterized not only by similar intensities but also by the proximity of the pixels. In Figure 2.7, for example, the lung region is surrounded by tissue with higher intensity values. Outside the patient’s body is air with intensity values similar to those of the lung. Unless the connectivity of the lung region is taken into account, intensity-based thresholding cannot separate the lung region from the air outside the patient. Two adjacent feature pixels are considered connected and therefore considered belonging to the same region. Two possible definitions of connectedness exist: 4-connectedness, where only neighbors to the north, west, east, or south are considered to be connected and diagonal pixels are not connected, and 8-connectedness, where all eight neighbors of a pixel, including the diagonal neighbors, are considered to be connected. For connected regions, region growing is a suitable segmentation method that is almost unsupervised. Region growing requires a threshold criterion and one or more seed points. Seed points may be provided interactively or may be special points determined by local criteria (local maxima) or geometry. The four (or eight) neighbor pixels of each seed point are examined, and each neighbor pixel that meets the threshold criterion is added to the feature set and in turn becomes a seed point. This algorithm lends itself to an elegant recursive implementation called floodfilling, but for large areas, particularly for a three-dimensional version of the algorithm, the allowable software stack memory size may be exceeded. In this case, it is necessary to scan the entire image iteratively and add neighbor pixels to the feature set until no more pixels are added between iterations. An example implementation of the region-growing algorithm is provided in Algorithm 2.4. This example assumes 8-connectivity and implements a simple threshold condition where all pixel candidates for region growing need to exceed a specified threshold value. This threshold condition can easily be extended to include multiple thresholds or even additional conditions such as a range of the local variance. A demonstration of the effect of region growing is given in Figure 2.10. Both lungs and the air region that surrounds the patient are separated by tissue with higher CT values. Therefore, the lungs and the surrounding air are not connected and can readily be separated by region growing.
Some methods to find an optimum threshold automatically, most notably Otsu’s method,17 can readily be extended to provide multiple thresholds. Equations (2.30) and (2.31) would be extended to reflect h classes and h – 1 thresholds [in Equation (2.36), n = 3], and the within-class variance to be minimized becomes
Algorithm 2.4 Region growing. Two images need to be provided: IM(x,y) as the image to be segmented, and MASK(x,y), which initially contains zero-valued pixels with the exception of the seed points, where the pixels have a value of 1. Region growing starts from these seed points for regions with image values above a threshold T, and the output is stored in MASK(x,y). Both images have the size xmax and ymax. Alternating the search direction between iterations accelerates the region-growing process considerably.
FIGURE 2.10 Demonstration of the difference between intensity-based thresholding (A) and region growing (B). Intensity-based thresholding does not make use of the connectedness of the region, and the air region outside the patient is incorrectly classified as belonging to the feature (white-striped area in A). Conversely, region growing that started with a seed point inside the right lung limits the feature to pixels connected to the seed pixel (horizontally striped region in B). A similar operation with the seed point inside the left lung then region-grows the entire left lung (vertically striped region in B).
Hysteresis Thresholding
Hysteresis thresholding is closely related to region growing. For hysteresis thresholding, two threshold values, T1 and T2, need to be defined where T1 > T2. Each pixel with I(x,y) > T1 is selected as a seed point, and from each seed point, region growing is performed with the constraint that I(x,y) > T2. In other words, hysteresis thresholding extracts connected regions where all image values are brighter than T2 but which must contain at least one pixel brighter than T1. The hysteresis is the difference T1 -T2. The effect of hysteresis thresholding is demonstrated in Figure 2.11 on a sample image from the Visible Human data set. Figure 2.11A shows the luminance channel of a photograph of the abdominal section where the goal was the segmentation of the adipose tissue of the torso only. Adipose tissue has the highest luminance value, but conventional thresholding (T = 152) leaves some adipose tissue from the extremities in the image, and several small pixel clusters within the muscle tissue are also classified as feature pixels (Figure 2.11B). With hysteresis thresholding (T1 = 224 and T2 = 152), only regions connected to the brightest pixels, which lie inside the torso, remain (Figure 2.11C). A similar result can be obtained by region growing with a pixel inside the torso as a seed pixel, but hysteresis thresholding acts in an unsuper-vised manner. Hysteresis thresholding can be implemented very easily. Algorithm 2.5, in combination with Algorithm 2.4, performs hysteresis thresholding by creating a mask of seed pixels from the higher threshold value T1. This step is followed immediately by Algorithm 2.4, which uses the variables created by Algorithm 2.5 and performs region growing from all initial seed pixels.
FIGURE 2.11 Comparison of conventional and hysteresis thresholding. Image A shows the luminance channel of a slice from the Visible Human data set. The brightest regions are adipose tissue. Conventional thresholding (B) classifies all adipose tissue, including tissue in the arms and some small clusters in the muscles, as feature pixels, whereas hysteresis thresholding (C) makes use of the connectedness constraint and accepts only adipose tissue from the torso as a feature.
Algorithm 2.5 Hysteresis thresholding. The input image is IM(x,y) with size xmax and ymax. This algorithm prepares the initial seed pixels in MASK(x,y) by simple thresholding with T1. It is followed immediately by Algorithm 2.4 for the region-growing process where T = T2.
