Geoscience Reference
In-Depth Information
11.3.3. Small Interfacial Waves
Since the critical (local) Richardson number depends on
the interface thickness in shear,
δ
v
, and density,
δ
ρ
, dif-
fusive effects are expected to play an important role for
the wavelength and growth of these instabilities. When
the interface ratio
R
=
δ
v
/δ
ρ
exceeds a certain threshold,
Hölmböe instability instead of Kelvin-Helmholtz instabil-
ity is possible. Generally,
R >
2 is needed for Hölmböe
instability to occur. Diffusion largely affects the inter-
face thicknesses, especially when the Reynolds number is
low, and entrainment is not efficient enough to erode the
diffused interface to a certain thickness. Stratified shear
instabilities satisfy the general Miles criterion [
Miles
,
1961, 1963]. If we define the gradient Richardson number,
Ri
(z)
=
N
2
/(dU/dz)
2
,where
N
2
(z)
=
Small-scale waves are observed in the different stages
of the experiments reported in various papers on fronts
in differentially rotating fluids [
Lovegrove et al.
, 2000;
Williams et al.
, 2005;
Flór et al.
, 2011] (see Figure 11.3).
The nature of these waves has been a major question and
has been debated in particular as a response to the paper
of
Williams et al.
[2005]. The different candidates that
have been considered are adjustment waves, spontaneous
emitted inertia-gravity waves [
McIntyre
, 2009], waves due
to Kelvin-Helmholtz or Hölmböe instability, and more
recently also the instabilities of the boundary layer at
the inner cylinder [
Jacoby et al.
, 2011] and the interfa-
cial Ekman boundary layer [
Jacoby
, 2012]. Here we briefly
review each of these wave types and subsequently focus on
experiments in an annulus with a tanh density profile.
Adjustment waves occur when an initially imbalanced
flow, during its transient process of adjustment toward a
newly balanced geostrophic flow, radiates inertia-gravity
waves [
Reznik et al.
, 2001]. Initially equilibrated flows
may also radiate inertia-gravity waves, even though the
flow is well described by the quasi-geostrophic equations.
The emission of these ageostrophic waves are due to a
“spontaneous imbalance,” a process that may refer to
different nonlinear mechanisms. First, these waves can
indeed be emitted via a mechanism that is similar to
the generation of noise in turbulent flow as described
by Lighthill's theory for acoustics. Their radiation have
been worked out for the shallow-water equations by
Ford
[1994]. Another mechanism of wave radiation that has
been suggested [
Vanneste and Yavneh
, 2004] is due to
advection: It induces a coupling between equilibrated
motion and inertia-gravity waves by a Doppler shift effect.
When gravity waves have a smaller length scale than the
balanced motion, the previous mechanisms cannot work
since they describe waves with wavelengths of the same
order as the large-scale balanced motion. The presence
of waves in idealized simulations of baroclinic life cycles
in continuously stratified flows [
O'SullivanandDunkerton
,
1995] is due not to the spontaneous emission of inertia-
gravity waves mentioned above but to the nonlinear devel-
opment of the baroclinic instability and the particular
environment of the flow with strong horizontal defor-
mation and large vertical shear [
Plougonven and Snyder
,
2005]. In particular, the vertical shear influences the prop-
agation of wave packets. Long waves may either break or
be absorbed. This wave capture phenomenon is relevant in
shearlowsandlocalwavesourcessuchas,forinstance,the
radiation by a dipolar vortex in a continuously stratified
fluid [
Snyder et al.
, 2007]. The amplitude of these waves is
still small compared to the waves due to shear instabilities.
In order to know whether the observed waves are due
to shear, we have to consider the Richardson number.
(g/ρ
0
)(∂ρ/∂z)
is
the Brunt-Väissälä frequency with a reference density
ρ
0
,
this criterion states stability for Ri
(z)
−
1
4
everywhere in
the profile and instability for Ri
(z)<
4
. Since gradients
are difficult to measure, generally the bulk Richardson
number
J
is used for experimental predictions. Follow-
ing Hölmböe [
Hölmböe
, 1962;
Lawrence et al.
, 1991;
Ortiz
et al.
, 2002;
Tedford et al.
, 2009;
Carpenter
, 2009], one can
write the dimensionless numbers
≥
gρ δ
v
ρ
0
(U)
2
,
R
δ
v
δ
ρ
2
d
δ
v
≡
≡
≡
J
,
a
,
where
ρ
0
=
(ρ
1
+
ρ
2
)/
2,
ρ
=
ρ
2
−
U
1
,and
a
is a potential shift of the center of the velocity profile.
For an inviscid Boussinesq fluid, the stability of a stratified
shear flow is then given by the Taylor-Goldstein equation
[e.g.,
Hazel
, 1972;
Pouliquen et al.
, 1994;
Alexakis
, 2005,
2007, 2009].
For simplicity, it is generally assumed that
δ
v
ρ
1
,
U
=
U
2
−
δ
ρ
,
allowing for an idealized model with piecewise constant
velocity profile and a jump in density (as in
Ortiz et al.
[2002]) and illustrated in Figure 11.8a. In such a piece-
wise model,
J
keeps the same definition, whereas
a
=0and
(a)
(b)
ρ
0
)
U
0
ρ
0
)
U
0
ρ
(
z
)
U
(
z
ρ
(
z
)
U
(
z
δ
υ
δ
ρ
δ
υ
Δ
U
Δ
ρ
Δ
U
Δ
ρ
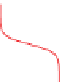
Figure 11.8.
Density and velocity profiles in a stratified shear
layer: (a) modelization with piecewise profiles; (b) hyperbolic
tangent profiles.