Information Technology Reference
In-Depth Information
a
2
l
s
l
t
l
s
l
t
l
s
l
t
a
1
a
2
a
1
a
1
a
h
a
2
ʸ
s
ʸ
ʸ
s
s
t
t
t
(a)
(b)
(c)
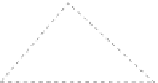
Fig. 4.
Illustration for the proof that
a
1
a
2
is a
ʸ
-edge
that there exists a
ʸ
-edgeincidentto
s
,assuch an edgeisalsoa
ʸ
-path starting at
s
,and
the existence of a
ʸ
-path starting at
s
implies the existence of a maximal
ʸ
-path starting
at
s
. Consider a straight-line segment
e
ʸ
that is the intersection of a directed half-line
incident to
s
with slope
ʸ
and of a disk of arbitrarily small radius centered at
s
.If
e
ʸ
is
internal to
H
P
, then consider the two edges
e
1
and
e
2
of
G
that are encountered when
counter-clockwise and clockwise rotating
e
ʸ
around
s
, respectively. Then,
e
1
or
e
2
is
a
ʸ
-edge, as the angle spanned by a clockwise rotation bringing
e
1
to coincide with
e
2
is smaller than 90
ⓦ
, given that
G
is a Gabriel triangulation, and
e
ʸ
is encountered
during such a rotation. If
e
ʸ
is outside
H
P
,whichmight happen if
s
on the boundary
H
P
,thenassume that the slope of
e
ʸ
is in the interval [0
ⓦ
;45
ⓦ
] (the case in which
the slope of
e
ʸ
is in the interval [
of
45
ⓦ
;0
ⓦ
] is analogous). Then, the angle spanned by a
clockwise rotation bringing
e
ʸ
to coincide with
st
is at most 45
ⓦ
.Since
st
is in interior
or on the boundary of
−
H
P
,anedge
e
1
of
G
is encountered during such a rotation, hence
e
1
is a
ʸ
-edge. An analogous proof shows that, for
every
ʸ
in the interval [
−
45
ⓦ
;45
ⓦ
],
there exists a maximal (
ʸ
+ 180
ⓦ
)-path starting at
t
that is low or high.
Second, we prove that, for
some
ʸ ∈
[
−
45
ⓦ
;45
ⓦ
], there exist a maximal low
ʸ
-path
and
a maximal high
ʸ
-path both starting at
s
. All the maximal (
−
45
ⓦ
)-paths (all the
maximal (45
ⓦ
)-paths) starting at
s
are low (resp. high), given that every edgeonthese
paths has slope in the interval [
90
ⓦ
;0
ⓦ
] (resp. [0
ⓦ
;90
ⓦ
]). Thus, let
ʸ
be the smallest
−
45
ⓦ
;45
ⓦ
] such that a maximal high
ʸ
-path exists. We prove
that there also exists a maximal low
ʸ
-path starting at
s
. Consider an arbitrarily small
>
0.Byassumption, there exists no high (
ʸ
constant in the interval [
−
−
)-path. Hence, from the previous
argument there exists a low (
ʸ
−
)-path
P
.If
is sufficiently small, then no edgeof
P
45
ⓦ
−
45
ⓦ
).Thuseveryedgeof
has slope in the interval [
ʸ
−
;
ʸ
−
P
has slope in the
45
ⓦ
;
ʸ
+45
ⓦ
−
interval [
ʸ
is a maximal low
ʸ
-path starting at
s
.
Since there exist a maximal high
ʸ
-path starting at
s
, a maximal low
ʸ
-path starting
at
s
, and a maximal (
ʸ
+180
ⓦ
)-path starting at
t
that is low or high, it follows that there
exist a maximal
ʸ
-path
−
), hence
P
P
s
starting at
s
and a maximal (
ʸ
+ 180
ⓦ
)-path
P
t
starting at
t
that are both high or both low. This proves Claim 2 and hence the lemma.
Lemma 3 and Lemma 4 immediately imply the following.
Corollary 1.
Any Gabriel triangulation is increasing-chord.
We are now ready to state the main result of this section.
Theorem 1.
Let
P
be a pointsetwith
n
points. Onecan construct in
O
(
n
log
n
)
time
an increasing-chord planar graph
G
(
P
,S
)
such that
P
P
and
P
|∈
ↆ
|
O
(
n
)
.