Information Technology Reference
In-Depth Information
P
1
(
d
)
p
b
(
d
)
p
a
(
d
)
d
P
2
(
d
)
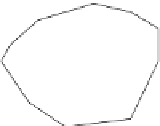
Fig. 5.
Subsets
P
1
(
d
) and
P
2
(
d
) of a point set
P
determined by a directed straight line
d
Proof.
Bern, Eppstein, and Gilbert [3] proved that, for any point set
P
, there exists a
point set
P
with
P
O
(
n
) such that
P
admits a Gabriel triangula-
tion
G
.Both
P
and
G
can be computed in
O
(
n
log
n
) time [3]. By Corollary 1,
G
is
increasing-chord, which concludes the proof.
P
and
P
|∈
ↆ
|
) Steiner points are not always enoughtoaugment a point set
P
to a point set that admits a Gabriel triangulation. Namely, consider any point set
B
with
O
(1) points that admits no Gabriel triangulation. Construct a point set
P
outof
We remark that
o
(
|
P
|
|
copies of
B
placed “far apart” from each other, so that any triangle with two points in
different copies of
B
is obtuse. Then, a Steiner point has to be added inside the convex
hull of each copy of
B
to obtain a point set that admits a Gabriel triangulation.
|
P
|
/
|
B
4
Increasing-Chord Convex Graphs with Few Edges
In this section we prove the following theorem;
Theorem 2.
Fo r every convex pointset
P
with
n
points, there exists an increasing-
chord geometric graph
G
(
P,S
)
such that
|
S
|∈
O
(
n
log
n
)
.
The main idea behind the proof of Theorem 2 is that any convex point set
P
can
be decomposed into some one-sided convex point sets
P
1
,...,P
k
(which by Lemma 1
admit increasing-chord spanninggraphs with linearly many edges) in such a way that
every two points of
P
are part of some
P
i
and that
|
is small. In order to perform
such a decomposition, we introduce the concept of
balanced
(
d
1
,
d
2
)
-partition
.
Let
P
be a convex point set and let
d
be a directed straight line not orthogonal to
any line through two points of
P
.SeeFig.5.Let
p
a
(
d
) and
p
b
(
d
) be the minimumand
maximum point of
P
with respect to
d
, respectively. Let
P
1
(
d
) be composed of those
points in
P
that are encountered when clockwise walking along the boundary of
P
i
|
H
P
from
p
a
(
d
) to
p
b
(
d
),where
p
a
(
d
)
P
1
(
d
).Analogously, let
P
2
(
d
)
be composed of those points in
P
that are encountered when clockwise walking along
the boundary of
∈
P
1
(
d
) and
p
b
(
d
)
/
∈
P
2
(
d
).
Let
d
1
and
d
2
be two directed straight lines not orthogonal to any line throughtwo
points of
P
, where the clockwise rotation that brings
d
1
to coincide with
d
2
is at most
180
ⓦ
.The(
d
1
,
d
2
)
-partition
of
P
partitions
P
into subsets
P
a
=
P
1
(
d
1
)
H
P
from
p
b
(
d
) to
p
a
(
d
),where
p
b
(
d
)
∈
P
2
(
d
) and
p
a
(
d
)
/
∈
∩
P
1
(
d
2
),