Graphics Reference
In-Depth Information
This method for computing the arc-length parameterization seemed to work well for
[ShaT82] and had no problems with convergence.
Sometimes one needs both arc lengths and arc-length parameterizations. In that
case one can use the arc-length algorithm from [GueP90]. The table (u
j
,s
j
) described
earlier not only helps with arc length but also with arc-length parameterization. If we
want to find u so that L(a,u) = s, then we find the j so that s
j
£ s < s
j+1
. This will tell
us that u Π[u
j
,u
j+1
] and give us a much better starting point for the Newton-Raphson
method applied to (14.26) so that it will run faster.
A problem related to finding the arc length of a curve is to find a curve between
two points that has specified tangent lines at the endpoints and also has a specified
length. See [RouB96a] and [RouB96b].
14.9
Offset Shapes
14.9.1
Offset Curves
To
offset
a curve or surface traditionally means to move the original a certain distance
along a normal vector. Here we are thinking of the curve or surface as lying in
R
3
and
the normal vector being a vector in
R
3
. One can define a more intrinsic notion,
however, and the engulfing space does not have to be
R
3
. For example, given a curve
in some surface
S
, one can define the offset of that curve
in S
. This would be gotten
by moving that curve along geodesics in
S
that are orthogonal to the original curve.
Such offsets are called
geodesic offsets
. A good overview of the literature on offset
curves and surfaces can be found in [Pham92] and [Maek99]. See also [Brec92].
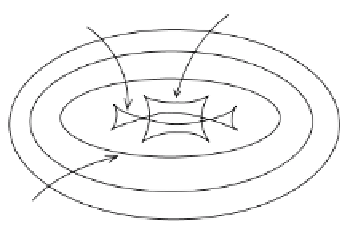
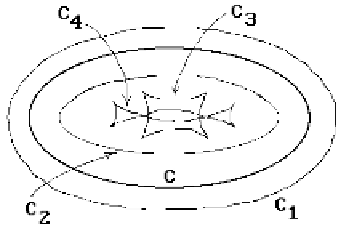
In general, getting an offset may involve stretching or shrinking the original.
Figure 14.34 shows an ellipse
C
and four offset curves
C
i
. Offsets are interesting also
in cases where the original object is not smooth but has differentiability discontinu-
ities. Figures 14.35(a) and 14.36(a) show offset curves when there are cusps and
corners. The offsets that are probably desired are shown in Figures 14.35(b) and
14.36(b). To get them one has to do some trimming and blending.
Offset curves are in general computationally more complicated than the original
curve. This is basically caused by the fact that one needs to take a square root to get
a unit normal vector. For example, except for special cases, the offset of a polynomial
or rational curve is not a polynomial or rational curve.
Figure 14.34.
Offset curves for an ellipse.