Graphics Reference
In-Depth Information
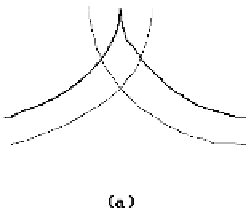
Figure 14.35.
Offset curves when there are cusps.
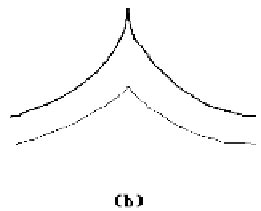
Figure 14.36.
Offset curves when there are corners.
This section will look at some of the mathematics behind offset curves and how
it can be used to solve practical problems. The reader is assumed to have familiarity
with some basic differential geometry. The necessary background can be found in
Chapter 9 in [AgoM05]. In particular, see Section 9.7 in that chapter on parallel curves
(that is what offset curves are called in differential geometry) for proofs of many of
the mathematical assertions made here.
Offset curves are useful tools in a number of practical applications, such as in
milling operations, tolerance analysis, and robot path planning. We shall start our dis-
cussion of analytic properties of offset curves by considering those of planar curves.
This is what is relevant for describing the path of a two-axis NC machine that can
move in two orthogonal directions (say the x- and y-direction). Such machines are
commonly used to cut two-dimensional outlines in materials. See Figure 14.37. Two
serious problems for them are
local overcuts
(
gouging
) or
local undercuts
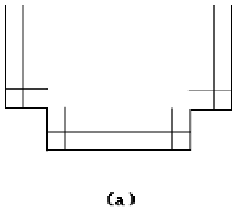
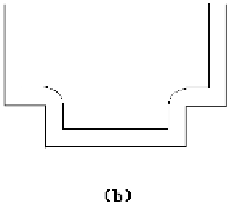
. Figure
14.38(a) shows a gouging example. As described in [MaeP93], the problem is that in
regions where the curvature and the signed offset distance have opposite signs, the
cutter radius must be smaller than any radius of curvature of the boundary curve of
the part being machined. If we simply eliminate the part of the cutter path that started
and ended at the intersection point of the offset curve, then we eliminate the overcut,
but will now have produced an undercut. See Figure 14.38(b).
Let p(u) = (x(u),y(u)) be a regular parameterization of a curve
C
in the plane. The
vector
1
()
=
¢
()
-
()
¢
()
(
)
nu
yuxu
,
pu