Graphics Reference
In-Depth Information
¢
()
=
(
()
)
¢
()
p u
DP d u d u .
This fact and induction leads to a proof of equation (11.87). The uniqueness of P
follows from the derivative formula (11.87).
Note.
The term “polar form” comes from mathematics. The term “blossom” was
introduced by Ramshaw in [Rams88]. A polynomial can be recovered from its
blossom.
11.5.2.2 Example.
A classical example of a blossom is the dot product function
P(
u
,
v
) =
u
•
v
in
R
n
, which is the blossom of the length squared function p(
v
) = |
v
|
2
.
11.5.2.3
Example.
The blossom of the cubic polynomial
()
=+ +
2
2
3
pu
a
au a u
+
a u
01
3
is
(
)
=+
(
)
(
)
+
(
)
(
)
+
Pu u u
,
,
a
a
3
u
++
u
u
a
3
uu
+
uu
+
u u
a uu u
.
1
2
3
0
1
1
2
3
2
1
2
1
3
2
3
3
1
2
3
What is the point of all of this? Replacing a polynomial of degree k with a func-
tion in k variables that is linear in each variable turns out to be very useful. We shall
see that it is another example of how nonlinear problems can be solved by lineariz-
ing them. To see what is going on here we look at a simple example.
11.5.2.4
Example.
Consider the function
()
=
2
pu
31
u
.
on [0,1] which has blossom
(
)
=
pu u
,
3
uu
+
1
.
12
12
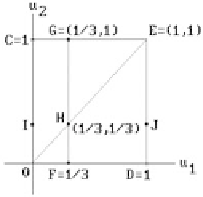
Suppose that we want to compute p(1/3). If D is the diagonal map D(u) = (u,u), then
p(u) = P(D(u)). See Figure 11.22. Let
A
,
B
,...be the points as indicated in the figure.
Figure 11.22.
How blossoming linearizes maps.