Graphics Reference
In-Depth Information
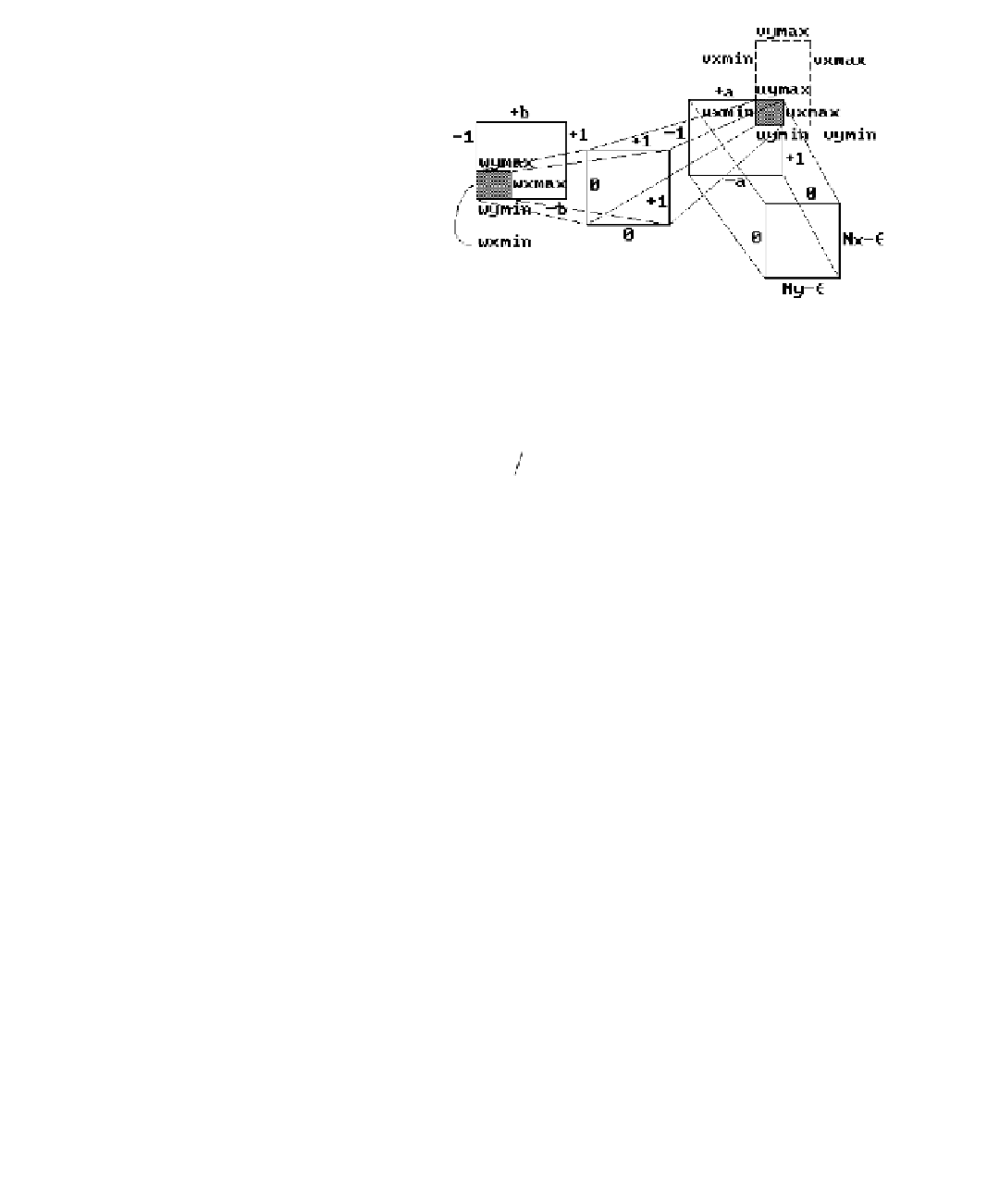
Figure 4.14.
General window and
viewport example.
[
]
¥
[
]
vpx
min,
vpx
max
vpy
min,
vpy
max
be the current viewport. Then
fix
the window to be the rectangle [-1,1] ¥ [-b,b], where
(
)
(
)
bry
=
max
-
y
min
x
max
-
x
min .
h
Now map directly from [0,1] ¥ [0,1] to pixel space. With this window and the view
transformations discussed in this chapter, circles will look like circles.
We close with a final remark on clipping. Clipping is expensive and therefore we
would rather not do it! In future chapters we shall discuss ways one can often avoid
it (by using bounding boxes, the convex hull property of splines, etc.).
4.8
Stereo Views
Occasionally, it is useful to allow the origin of the view plane to be a point other than
the one directly in front of the camera. One such case is where one wants to compute
stereo views. This involves computing two views, one for each eye.
The Eye Coordinate System.
Given a camera, let (
u
1
,
u
2
,
u
3
,
p
) be the camera coor-
dinate system, where the vectors
u
1
,
u
2
, and
u
3
are defined by equation (4.1) If
we think of one eye as being located at
p
+ a
u
1
+ b
u
2
, then the eye coordinate system
with respect to the given camera and some a, b Œ
R
is defined by the frame
(
u
1
,
u
2
,
u
3
,
p
+ a
u
1
+ b
u
2
). If a = b = 0, then this is the same as the camera coordinate
system.
It is easy to see that if the coordinates of a point
p
in camera coordinates is (x,y,z),
then the coordinates of that same point in eye coordinates are (x - a,y - b,z). Fur-
thermore, if
p
projects to (x¢,y¢,d) in eye coordinates, then it projects to (x¢+a,y¢+
b,d) in camera coordinates. It follows that, using homogeneous coordinates, the only
difference in computing the view in camera coordinates to computing it in eye coor-
dinates amounts to replacing the matrix M
persp
in equation (4.9) by