Graphics Reference
In-Depth Information
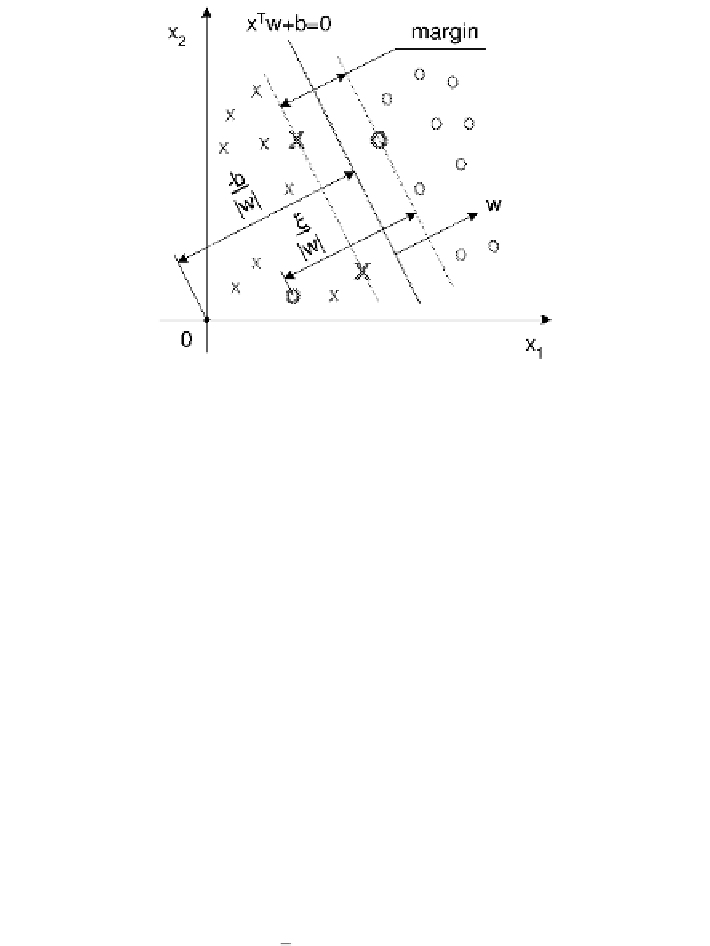
Figure
.
.
he separating hyperplane x
w
and the margin in an inseparable case. he
observations marked with bold crosses and zeros are support vectors. he hyperplanes bounding the
margin zone (which are equidistant from the separating hyperplane) are represented as x
w
+
b
=
+
b
=
and x
w
+
b
=−
bythelinearSVMisahyperplanesymmetrically surroundedbyamarginzone.Itcan
beshown(Härdleetal.,
a)that thecomplexity ofsuchaclassifier canbereduced
bymaximizing the margin. By applying kernel techniques, the SVM can be extended
to learn nonlinear classifying functions (Fig.
.
).
In Fig.
.
, misclassifications are unavoidable when linear classifying functions
are used (linearly inseparable case). To account for misclassifications, the penalty ξ
i
is introduced, which is related to the distance from the hyperplane bounding obser-
vations of the same class to observation i. ξ
i
if a misclassification occurs. All
observations satisfy the following two constraints:
x
y
i
(
i
w
+
b
)
−
ξ
i
,
(
.
)
ξ
i
.
(
.
)
With the normalisation of w, b and ξ
i
asshownin(
.
),themarginequals
.
he convex objective function to be minimised given the constraints (
.
) and (
.
)
is:
w
n
i
=
w
+
C
ξ
i
.
(
.
)
heparameterC,calledthecapacity,isrelatedtothewidthofthemarginzone.Larger
marginsbecomepossibleasthevalueofC decreases. Using awell-established theory
for the optimisation of convex functions (Gale et al.,
), we can derive the dual
Lagrangian
n
i
=
n
i
=
n
i
=
n
i
=
w
L
D
=
(
α
)
w
(
α
)−
α
i
−
δ
i
α
i
+
γ
i
(
α
i
−
C
)−
β
α
i
y
i
(
.
)