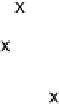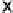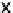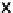Graphics Reference
In-Depth Information
Figure
.
.
Mapping from a two-dimensional data space to a three-dimensional space of features
R
R
using a quadratic kernel function K
x
i
x
j
. he three features correspond to the
(
x
i
, x
j
)=(
)
=
x
, x
x
. he transformation is thus
three components of a quadratic form: x
=
x
x
,and x
=
.hedatathatareseparableinthedataspacewithaquadraticfunction
will be separable in the feature space with a linear function. A nonlinear SVM in the data space is
equivalent to a linear SVM in the feature space. he number of features will grow rapidly with the
dimensionality d and the degree of the polynomial kernel p, which is
in our example, making the
closed-form representation of Ψ such as that shown here practically impossible
x
,
x
x
, x
Ψ
(
x
, x
)=(
)
for the dual problem:
min
α
i
,δ
i
,γ
i
,β
max
w
k
,b,ξ
i
L
D
.
(
.
)
Here, for a linear SVM,
n
i
=
n
j
=
α
i
α
j
y
i
y
j
x
w
(
α
)
w
(
α
)=
i
x
j
.
(
.
)
A more general form is applicable in order to obtain nonlinear classifying functions
in the data space:
n
i
=
n
j
=
w
α
w
α
α
i
α
j
y
i
y
j
K
x
i
, x
j
(
.
)
(
)
(
)=
(
)
hefunction K
iscalledakernelfunction.Sinceithasaclosedformrepresen-
tation, the kernel is a convenient way of mapping low-dimensional data into a highly
dimensional (oten infinitely dimensional) space of features. It must satisfy the Mer-
cer conditions (Mercer,
),i.e. it must be symmetric and semipositive definite; in
other words it must represent a scalar product in some Hilbert space (Weyl,
).
In our study, we applied an SVM with an anisotropic Gaussian kernel
(
x
i
, x
j
)
r
−
Σ
−
K
(
x
i
, x
j
)=
exp
−(
x
i
−
x
j
)
(
x
i
−
x
j
)
(
.
)
where r is a coe
cient and Σis a variance-covariance matrix. he coe
cient r is
related to the classifying function complexity: as r increases, the complexity drops.If