Graphics Reference
In-Depth Information
1.0
0.8
0.6
0.4
0.2
0.0
−
0.2
0.0
0.5
1.0
t
1.0
b
0.8
0.6
0.4
0.2
0.0
−
0.2
−
2.5
−
2.0
−
1.5
−
1.0
−
0.5
0.0
0.5
1.0
1.5
2.0
2.5
t
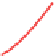
Figure 22.7: The four Catmull-Rom basis functions, plotted on a single coordinate system,
and then shifted and assembled to form the function b
CR
defined on the interval
[
−
2, 2
]
.
Because b
CR
is continuous and is C
1
smooth, so is the Catmull-Rom spline. Because
b
CR
(
0
)=
1
, while b
CR
(
i
)=
0
for all other integers i, the Catmull-Rom spline is inter-
polating.
p
1
(
t
)=
1
t
3
+
2
t
2
2
(
−
−
t
)
p
2
(
t
)=
1
2
(
3
t
3
5
t
2
+
2
)
−
p
3
(
t
)=
1
3
t
3
+
4
t
2
+
t
)
, and
2
(
−
p
4
(
t
)=
1
2
(
t
3
t
2
)
.
−
The form of the Catmull-Rom curve given in Equation 22.9 is convenient
for studying the properties of Catmull-Rom splines. Note that, although the sum
appears to have
n
terms, for any particular value of
t
there are, at most, four
nonzero terms. This means that it's easy to write code to rapidly determine points
on a Catmull-Rom spline. The function
b
CR
goes below 0 at some times. This
means that the sum in Equation 22.9 is not a
convex
combination of the control
points: The interpolating curve for control points
P
o
,
,
P
n
may go outside the
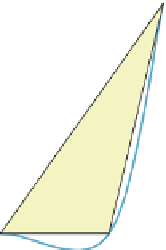
convex hull of these points. Figure 22.8 shows a simple example. It's a sad fact
that if you want a smooth
interpolating
curve (i.e., one that passes
through
the
control points rather than near them), this failure to stay within the convex hull is
unavoidable.
Note that the function
b
CR
is infinitely differentiable at most points (because
it's polynomial), but at the joint points (
x
=
...
Figure 22.8: The Catmull-Rom
spline for three control points lies
almost entirely outside the yel-
low triangular convex hull of the
three points.
−
2,
−
1, 0, 1, 2) it's only
once