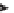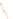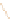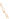Graphics Reference
In-Depth Information
Figure 10.4 shows the effects of
T
4
. It distorts the house figure, but not by just a
rotation or scaling or shearing along the coordinate axes.
Example 5: A degenerate (or singular) transformation
Let
x
R
2
:
x
y
1
x
y
=
x
.
−
1
−
y
T
5
:
R
2
→
→
(10.7)
2
−
2
2
x
−
2
y
Before
Figure 10.5 shows why we call this transformation
degenerate:
Unlike the
others, it collapses the whole two-dimensional plane down to a one-dimensional
subspace, a line. There's no longer a nice correspondence between points in the
domain and points in the codomain: Certain points in the codomain no longer
correspond to
any
point in the domain; others correspond to
many
points in the
domain. Such a transformation is also called
singular,
as is the matrix defining it.
Those familiar with linear algebra will note that this is equivalent to saying that
y
the determinant of
M
5
=
1
is zero, or saying that its columns are linearly
−
1
x
2
−
2
dependent.
After
Figure 10.4: A general transfor-
mation. The house has been quite
distorted, in a way that's hard to
describe simply, as we've done
for the earlier examples.
Here we'll describe several properties of linear transformations from
R
2
to
R
2
.
These properties are important in part because they all generalize: They apply
(in some form) to transformations from
R
n
to
R
k
for any
n
and
k
. We'll mostly be
concerned with values of
n
and
k
between 1 and 4; in this section, we'll concentrate
on
n
=
k
=
2.
y
Transformation
If
M
is a 2
×
2 matrix, then the function
T
M
defined by
x
T
M
:
R
2
R
2
:
x
→
→
Mx
(10.8)
is linear. All five examples above demonstrate this.
For nondegenerate transformations, lines are sent to lines, as
T
1
through
T
4
show. For degenerate ones, a line may be sent to a single point. For instance,
T
5
Before
sends the line consisting of all vectors of the form
b
b
to the zero vector.
Because multiplication by a matrix
M
is always a linear transformation, we'll
call
T
M
the
transformation associated to the matrix M.
y
Transformation
In
R
n
, it turns out that for
every
linear transform
T
, there's a matrix
M
with
T
(
x
)=
Mx
, which means that every linear transformation is a matrix transfor-
mation. We'll see in Section 10.3.5 how to find
M
,given
T
,evenif
T
is expressed
in some other way. This will show that the matrix
M
is completely determined
by the transformation
T
, and we can thus call it the
matrix associated to the
transformation.
x
After
Figure 10.5: A degenerate trans-
formation, T
5
.