Digital Signal Processing Reference
In-Depth Information
Example 2.7.6
Consider the random variable
X
from Example 2.7.5, where we
found
EfX
2
EfXg ¼
0
g ¼
5
=
2
:
(2.248)
;
The transformation of the variable
X
was a quadratic function (i.e., a nonlinear
function)
gðXÞ ¼ X
2
:
(2.249)
The corresponding mean value is:
g ¼ EfX
2
E gðXÞ
f
g ¼
5
=
2
:
(2.250)
However, the quadratic transformation of the mean value is:
2
¼
0
2
g EfXg
ð
Þ ¼ EfXg
ð
Þ
¼
0
:
(2.251)
Therefore,
EfgðXÞg 6¼
gðEfXgÞ:
(2.252)
2.7.3 Mean Value of a Continuous Random Variable
We can apply a similar approach to that used to derive the mean value of a discrete
random variable, in order to develop the expression for the mean value of a
continuous random variable. Consider the continuous random variable
X
with the
continuous range
x
from 0 to
A
(Fig.
2.40
). We divide the range
x
into
k
small
intervals
Dx
such that, if the random variable belongs to the
i
th interval [(
i
1)
Dx
,
iDx
], we can consider that it is equal to the end of the interval (i.e., equal to
iDx
).
In other words, if
Xe½ði
1
ÞDx; iDx
it means that
X ¼ i Dx
,
,
k
.
Imagine that we perform an experiment
N
times and that we obtain the number
of times that the variable
X
was in each of the intervals
iDx
,
i ¼
1,
i ¼
1,
...
,
k
:
...
X ¼ Dx
N
1
times,
X ¼
2
Dx
N
2
times,
...
...
X ¼ i Dx
N
i
times,
...
...
X ¼ k Dx
N
k
times
:
(2.253)
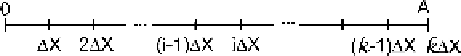
Search WWH ::

Custom Search