Graphics Reference
In-Depth Information
(
X
-
A
)
•
(
C
-
A
)
≤
0
B
VR
(
A
)
A
(
X
-
A
)
•
(
B
-
A
)
≤
0
C
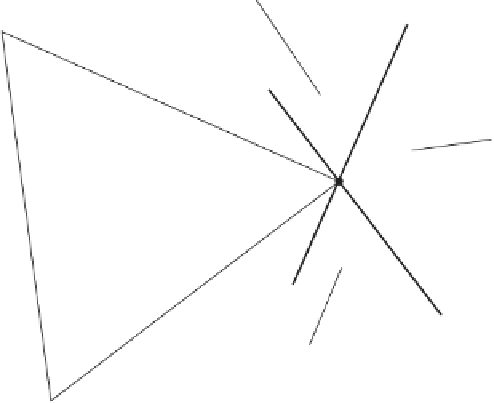
Figure 5.5
The Voronoi region of vertex
A
,
VR
(
A
), is the intersection of the negative halfspaces
of the two planes (
X
-
A
) · (
B
-
A
) = 0 and (
X
-
A
) · (
C
-
A
)=0.
Once determined, only the orthogonal projection of
P
onto the corresponding fea-
ture must be computed to obtain
Q
.
To see how
P
can be determined to be in a vertex Voronoi region, consider the
vertex Voronoi region of
A
. This region is determined as the intersection of the
negative halfspaces of two planes through
A
, one with a normal of
B-A
and the other
with the normal
C-A
(as illustrated in Figure 5.5).
Determining if
P
lies in one of the edge Voronoi regions can be done in a number
of ways. It turns out that an efficient test is to effectively compute the barycentric
coordinates of the orthogonal projection
R
of
P
onto
ABC
. Recall from Section 3.4
that the barycentric coordinates of
R
are given as the ratios of (anything propor-
tional to) the signed areas of triangles
RAB
,
RBC
, and
RCA
to the signed area of
ABC
. Let
n
be the normal of
ABC
and let
R
=
P
−
t
n
for some
t
. The barycen-
tric coordinates (
u
,
v
,
w
)of
R
,
R
=
uA
+
vB
+
wC
, can then be computed from the
quantities
Vector n = Cross(b - a,c-a);
float rab = Dot(n, Cross(a - r, b - r));
// proportional to signed area of RAB
float rbc = Dot(n, Cross(b - r, c - r));
// proportional to signed area of RBC
float rca = Dot(n, Cross(c - r, a - r));
// proportional to signed area of RCA
float abc = rab + rbc + rca;
// proportional to signed area of ABC