Error-Driven Task Learning - Computational Explorations in Cognitive Neuroscience - page 152

Sum Squared vs Cross Entropy Error

bias weight to decrease, and the unit to be less active.
Thus, the bias weight learns to correct any relatively
constant errors caused by the unit being generally too
active or too inactive.
From a biological perspective, there is some evidence
that the general level of excitability of cortical neurons
is plastic (e.g., Desai et al., 1999), though this data does
not specifically address the kind of error-driven mecha-
nism used here.

3.0

2.5 CE

SSE

2.0

1.5

1.0

0.5

0.0

0.0 0.2 0.4 0.6 0.8 1.0

5.4 Error Functions, Weight Bounding, and

Activation Phases

Output Activation (Target = 1)

Three immediate problems prevent us from using the
delta rule as our task-based learning mechanism; (1)
The delta rule was derived using a linear activation
function, but our units use the point-neuron activation
function; (2) The delta rule fails to enforce the biolog-
ical constraints that weights can be only either positive
or negative (see chapters 2 and 3), allowing weights to
switch signs and take on any value; (3) The target output
values are of questionable biological and psychological
reality. Fortunately, reasonable solutions to these prob-
lems exist, and are discussed in the following sections.

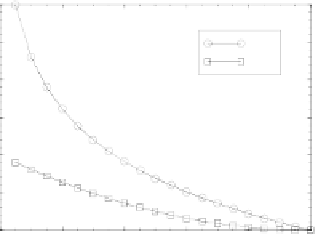
Figure 5.5: Comparison of the cross entropy (CE) and sum-
squared error (SSE) for a single output with a target value of
1. CE is larger, especially when the output is near 0.

measure for probability distributions. It is defined as:

)
(5.11)
where the actual output activation o k and the target ac-
tivation t k must be probability-like variables in the 0-1
range (and the target t k is either a 0 or a 1). The entropy
of a variable x is defined as x log x ,soCErepresentsa
cross entropy measure because it is the entropy across
the two variables of tk and ok , considered as both the
probability of the units being on (in the first term) and
their probabilities of being off (in the second term in-
volving 1 ￿ tk and 1 ￿ ok ).
Like the SSE function, CE is zero if the actual activa-
tion is equal to the target, and increasingly larger as the
two are more different. However, unlike squared error,
CE does not treat the entire 0-1 range uniformly. If one
value is near 1 and the other is near 0, this incurs an es-
pecially large penalty, whereas more “uncertain” values
around .5 produce less of an error (figure 5.5). Thus,
CE takes into account the underlying binary true/false
aspect of the units-as-detectors by placing special em-
phasis on the 0 and 1 extremes.
For convenience, we reproduce the net input and sig-
moid functions from chapter 2 here. Recall that the net
input term ￿ k accumulates the weighted activations of

5.4.1 Cross Entropy Error

At this point, we provide only an approximate solution
to the problem of deriving the delta rule for the point-
neuron activation function. Later in the chapter, a more
satisfying solution will be provided. The approximate
solution involves two steps. First, we approximate the
point neuron function with a sigmoidal function, which
we argued in chapter 2 is a reasonable thing to do. Sec-
ond, we use a different error function that results in the
cancellation of the derivative for the sigmoidal activa-
tion function, yielding the same delta rule formulation
derived for linear units (equation 5.9). The logic behind
this result is that this new error function takes into ac-
count the saturating nature of the sigmoidal function, so
that the weight changes remain linear (for the mathe-
matically disinclined, this is all you need to know about
this problem).
The new error function is called cross entropy (ab-
breviated CE; Hinton, 1989a), and is a distancelike