Cryptography Reference
In-Depth Information
shaped like
Figure 2-4(a)
. If 4a
3
+ 27b
2
= 0, then the curve will be shaped like
Figure 2-4(b)
;
however, in this
case, we have a double or even triple root, which tends to spoil some of the mathematics. We don't consider
this case when constructing any of our algorithms. Finally, if 4a
3
+ 27b
2
< 0, then the curve will be shaped as in
Figure 2-4
Elliptic curves in
2.6.1 Addition of Points
In order to do many of the elliptic curve cryptographic algorithms, we need to have some way to use these
curves. In fact, we are actually going to perform operations on the
points
that satisfy the curve equation.
We will do this by defining operations on the points. First, assume that a point is represented by its coordin-
ates,
P
= (
x, y
). We want to define the
negative
to a point by negating the
y
component (that is, taking 0 -
y
in
the appropriate field), so that -
P
= (
x
, -
y
).
We also want to define the addition of two points. Assume that we have two points,
P
= (x
1
, y
1
) and
Q
= (x
2
,
y
2
). Graphically, we want to calculate
P
+
Q
by the following construction:
1. Draw a line through
P + Q.
2. There will be a third intersection of the line with the elliptic curve, say, R.
3. The
sum of the two points
is then defined to be the negative of the third intersection, so that
P
+
Q
=
-R.
This definition of addition isn't too difficult to grasp. But as we can see in graphs of the curve, such as in
Figure 2-5
, we have some difficulties. What if we add together two points that are inverses of each other, that
is,
P
+ (-P)? Graphically, this creates a vertical line.
Figure 2-5
Elliptic curve addition of two points,
P
and Q.

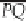
Search WWH ::

Custom Search