Cryptography Reference
In-Depth Information
This is where the point at infinity we mentioned comes into play. Graphically speaking, we want to include
the “top” of the y-axis as a virtual point on the curve, so that the vertical line “intersects” this point ∞. When we
work with non-graphically representable elliptic curves, such as those on finite fields, we merely have to treat
the point at infinity as a construct that helps us deal with these special cases.
We can also see that this point, given our usage thus far, fulfills the role of the algebraic identity, if we con-
sider the points on the elliptic curve together with addition as a potential group. This is exactly what we want!
We already have that
P
+ (-
P
) = ∞. It should also make sense that ∞ + ∞ = ∞, as well as ∞ = −∞. By our
construction, we can also see that
P
+ ∞ is found by drawing a vertical line through
P
, and finding the third
intersection, which will be -
P
. We take the inverse of -
P
, which is
P
, and thus
P
+ ∞ = P.
For more generic groups, we add this point at infinity to the potential group, with the previous properties
defined, since we can't have a more drawing-focused version — it's not very easy to “draw” lines if our field is
the integers 0-12.
Now, let's refine our above definition of addition of points to be more algebraically generic. When we draw a
line, that normally means taking the two points and writing an equation expressing a linear relationship between
the two points. Finding the third intersection is a matter of solving a system of two equations (one linear, one
cubic) and two unknowns, which it turns out has a general solution on a field.
For the following calculation of
P
+
Q,
assume that we have an elliptic curve represented by the points satis-
fying the equation
y
2
=
x
3
+
ax
+
b
in some field
F
, with
P
= (
x
1
,
y
1
) and
Q
= (
x
2
,
y
2
).
1. Check the special case
P
= -
Q
, in which case
P
+
Q
= ∞.
2. Check the other special case
P
= Q. In this case, our equation of
y
=
mx
+
c
is
tangent
to the curve
(intersects, but does not pass through). From calculus, we can calculate the derivative via implicit differ-
entiation of the curve at
P
as the slope of the tangent curve, which will be (3 +
a
) × (2
y
1
)
-1
.
Be very
careful here:
We are calculating the inverse of 2y
1
in the field; this does
not
mean division of integers or
real numbers.
3. If
P
≠
Q,
then we can calculate the slope the old-fashioned way:
m
= (y
2
-
y
1
) × (x
2
-
x
1
)
—1
(“rise over
run,” but on a field). Again,
be careful,
since we are not necessarily doing normal division.
4. We now need to calculate the value
c
(our
y
intercept). We have two equations:
We can solve for
c
by taking twice the first equation and subtracting the second equation, that is, 2 ×
5. We now want to solve for
P
+
Q
= (
x
3
,
y
3
) on the curve, thus we have two equations:
(2.3)
(2.4)
Substituting the first into the second, we get that (
mx
+
c
)
2
=
x
3
+
ax
+
b
, or
x
3
-
m
2
x2
+
(a
- 2
mc)x
+
(b
-
c
2
)
= 0. Now, this is not too much fun to factor. However, some basic algebra might conjure up
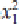

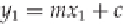

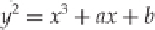
Search WWH ::

Custom Search