Cryptography Reference
In-Depth Information
The above boomerang attack lets us develop an attack using only the characteristic for the first half of the
cipher, bypassing the latter half. If sufficiently strong characteristics exist, then we have a good attack. We use
the characteristics just as before to derive the key. With the characteristic properly set in the final (and first)
rounds, we can brute-force the keys that affect the differential, measure it, and select the most likely candidate
key bits.
After this first layer is stripped away, we can continue developing characteristics to get more key bits, or just
perform an exhaustive search on the remaining key bits.
Wagner [20] uses exactly this premise against the COCONUT98 algorithm [18]. COCONUT98 has a 256-bit
key and was developed specifically to defeat differential cryptanalysis by having no useful characteristics. Des-
pite this, COCONUT98's key can be derived using the boomerang attack with 2
16
chosen plaintext-ciphertext
sets, with 2
41
offline computations (equivalent to 2
38
encryptions, according to Reference [20]).
In addition to its attack on COCONUT98, Reference [20] also mounts an incredibly successful attack against
FEAL (Section 4.7) and Khufu, a 64-bit block cipher with a 512-bit key [13].
7.15 Interpolation Attack
Many of these differential techniques are extensions of standard, continuous techniques of calculus, such as the
derivative. As a matter of fact, differentials are sometimes referred to as
derivatives
. The primary difference is
that, instead of applying the techniques to continuous spaces, like real or complex numbers, we are applying the
techniques to discrete spaces — in our case, integers between 0 and 2
n
.
Another technique many learn is
interpolation
: If we wish to find a line between two points, or a parabola
betweenthree,or,ingeneral,apolynomialofdegree
n
-1thatpassesbetween
n
points,thereisasimpleformula
to calculate this polynomial. These formulas can be used to analyze the relationship between various points or
to find additional points lying in between points.
For example, for a simple line between two points (
x
0
,
y
0
) and (
x
1
,
y
1
) we can see that the following line
includes both points:
If we plug in
x
0
, we get
y
0
, and if we plug in
x
1
, we get
y
1
. The function is linear because it contains only the
variable
x
.
In the general case, for points (
x
i
,
y
i
), for
i
= 1, ... ,
n
, our
interpolating polynomial
, ρ(
x
) is given by
This is merely an extension of our previous case to produce a polynomial of degree
n
- 1. This is called the
Lagrange interpolating polynomial
.
Thistechniquecanalsobeappliedtothediscreteworldofbitsandbytes,asshownbyJakobsenandKnudsen
[7]. We simply apply the above definitions to discrete functions, where the
x-
and
y
-values will be plaintext and
their associated ciphertexts, respectively.
We can apply this technique by noting that 32-bit XOR operations are identical to algebraic addition in the
finite field GF (2
32
) (since it has characteristic 2, i.e., 2 is equivalent to 0, so that 1 + 1 = 0).
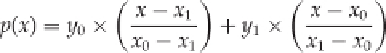
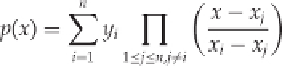
Search WWH ::

Custom Search