Graphics Reference
In-Depth Information
where c is a constant.
The parameterization q(s) in Equation (9.27) is not regular at a point of inflection
of p(s) because the derivative
¢
()
=
()
-
()
+-
(
)
¢
()
=-
(
) () ()
qs Ts Ts csTs
cs sNs
k
vanishes when k(s) = 0.
9.6.2. Theorem.
The curvature k* of the involute
C
* is given by
22
kt
+
k
*
=
.
2
2
(
)
cs
-
k
Proof.
See [Lips69].
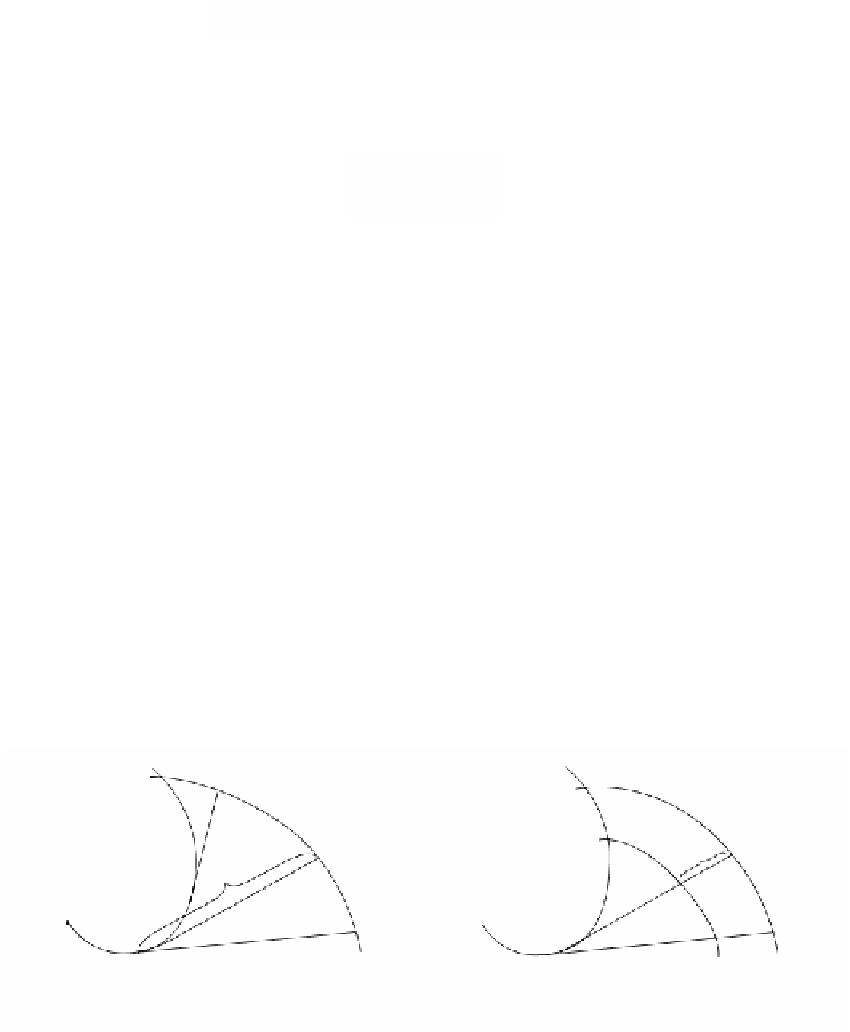
There is a nice geometric description of the involute. Assume that p(s) is defined
on the interval [0,c] and that we have wrapped a string of length c along the curve
C
starting at p(0) and ending at p(c). If we were to unwrap the string holding it taut,
then the end of the string generates the involute defined in equation (9.27). See Figure
9.12(a). Another fact that one can easily show is that the distance between two invo-
lutes is constant. See Figure 9.12(b).
Definition.
If a curve
C
* is the involute of a curve
C
, then
C
is called an
evolute
of
C
*.
Again, let p(s) be the arc-length parameterization of a curve
C
and (T(s),N(s),B(s))
its moving trihedron. Let
C
* be an evolute of
C
. There exist functions a(s) and b(s),
so that
()
=
()
+
() ()
+
() ()
qs
ps
a
sNs
b
sBs
(9.28)
is a parameterization of
C
*. The reason that there is no T(s) term is that, by defini-
tion, q(s) - p(s) is orthogonal to T(s). See Figure 9.13.
C
p(c)
p(c
2
)
C*
|c
2
- c
1
|
p(c
1
)
c- s
p(0)
p(0)
p(s)
C
*
*
C
2
C
1
(a)
(b)
Figure 9.12.
Generating involutes by unwrapping a string.