Graphics Reference
In-Depth Information
2
2
(
)
=-
(
)
(
)
a xyt
,,
x t
+-
y t
-=
10
.
(9.25)
Solution.
In this case, equation (9.24) reduces to
xy t
+=2
.
(9.26)
Eliminating t from (9.25) and (9.26) leads to
2
(
)
xy
-
=
2
,
which gives the same answer as in Example 9.5.2.
9.6
Involutes and Evolutes of Curves
Definition.
Given a curve
C
, the union of all tangent lines of
C
is called the
tangent
surface
of
C
. An
involute
of
C
is any curve that lies on the tangent surface of
C
and
that intersects all the tangent lines orthogonally.
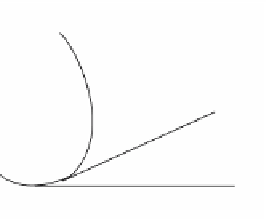
See Figure 9.11. Let p(s) be the arc-length parameterization of a curve
C
and
(T(s),N(s),B(s)) its moving trihedron. Let
C
* be an involute of
C
. By definition, there
is a function a(s), so that
()
=
()
+
() ()
qs
ps
a
sTs
is a parameterization of
C
*. Furthermore, q¢(s) is orthogonal to T(s), that is,
=
()
∑
()
=
(
()
+
() ()
+
()
¢
()
)
∑
()
=+
()
0
q s
Ts
Ts
a
sTs
a
sT s
Ts
1
a
s
.
This implies that a(s) =-s + c, for some constant c, proving
9.6.1. Theorem.
The involutes of a curve p(s) are precisely those curves that admit
a parameterization of the form
()
=
()
+-
(
) ( )
,
qs
ps
c sTs
(9.27)
C*
q¢(s)
C
q(s)
T(s)
p(s)
Figure 9.11.
An involute.