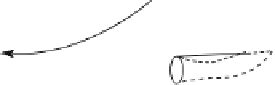Graphics Reference
In-Depth Information
6.5.10. Theorem.
The sphere, the connected sum of n tori, n ≥ 1, and the connected
sum of m projective planes, m ≥ 1, are nonhomeomorphic spaces.
Proof.
The proof follows easily from Proposition 6.5.9 and the topological invari-
ance of the Euler characteristic.
Theorems 6.5.7 and 6.5.10 together comprise what is called the classification
theorem for closed surfaces. This theorem can be summarized by the following:
Algorithm for determining the homeomorphism type of a given surface S:
Step 1:
Decide whether or not
S
is orientable.
Step 2:
Compute the Euler characteristic of
S
from a triangulation.
Step 3:
Look up the surface type in Table 6.5.2.
Computing the Euler characteristic is a simple counting procedure but determining
orientability is a little more subtle. The problem is that we do not yet have a formal
definition of orientability. We shall return to that point in the next chapter (Section
7.5).
If we do not count connected sums, then the only concrete example of a nonori-
entable surface that we have so far is the projective plane. There is another well-known
nonorientable surface, called the Klein bottle, named after the mathematician Felix
Klein who first described it. This surface is easier to visualize than the projective plane
and we finish this section with a brief discussion of it.
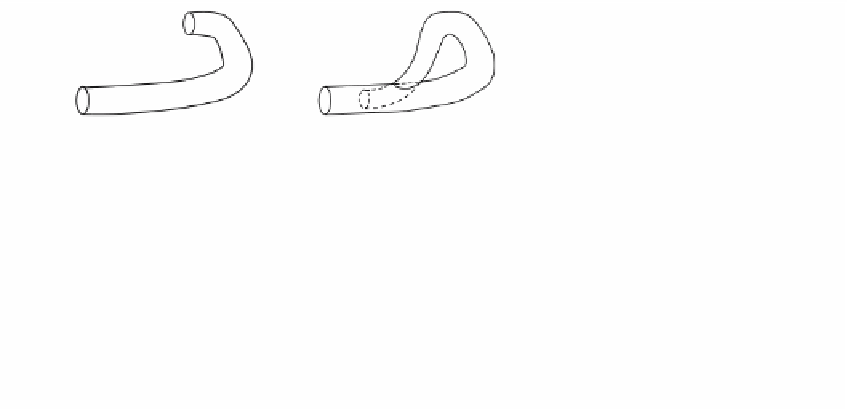
First, recall that to construct a torus one can start with a tube (Figure 6.17(b))
and then bring the ends around and glue them together (Figure 6.17(a)). We vary this
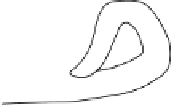
construction slightly. We again start with a tube (Figure 6.24(a)), but rather than
self-intersection X
(a)
(b)
(c)
A
2
A
1
A
1
A
2
(d)
Figure 6.24.
The Klein bottle.