Graphics Reference
In-Depth Information
4.7
Zeros of Functions
Many problems can be reduced to the problem of finding the zeros or roots of a func-
tion. This section discusses some basic approaches to solving this problem.
Given a function f :
R
n
Æ
R
m
, find a solution to
The Problem:
()
=
f
x0
.
(4.14)
The Newton-Raphson method:
We begin with the case where n = m = 1. Pick a
guess x
0
for a root. If this is not correct, then from the Taylor expansion formula we
know that
()
=
()
+¢
()
-
(
)
+
f x
f x
f
x
x
x
higher order terms
-
.
0
0
0
Forgetting the higher-order terms means that, as an approximation, we are looking
for an x so that
=
()
+¢
()
-
(
)
0
fx
f x
x x .
0
0
0
In other words,
=-
()
¢
()
fx
fx
0
0
xx
.
0
We use this x as the next guess at a solution to f(x) = 0. If we still do not have a root
we repeat this process, thereby generating a sequence of points x
0
, x
1
, x
2
,..., where
in general,
=-
()
¢
()
fx
fx
k
k
x
x
.
k
+
1
k
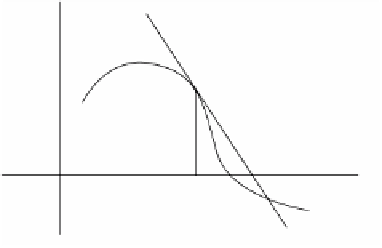
This sequence hopefully converges to a root. Figure 4.19 shows what is going on geo-
metrically. If x
k
is not a root, then find the intersection of the tangent line to the graph
of f(x) at (x
k
,f(x
k
)) with the x-axis. This point becomes our next guess x
k+1
.
f
(x
k
,f(x
k
))
x
k
x
k+1
Figure 4.19.
The Newton-Raphson method.