Java Reference
In-Depth Information
Things get worse. The call to
Fibonacci(n
-
1)
calls
Fibonacci(n
-
3)
as well. The two previous
calls to
Fibonacci(n
-
2)
each invoke
Fibonacci(n
-
3)
, so
Fibonacci(n
-
3)
is computed three
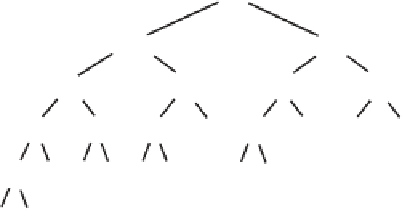
times. Figure 7-10a illustrates the dependency of
F
6
on previous Fibonacci numbers and so indicates the
number of times a particular number is computed repeatedly by the method
Fibonacci
. In contrast,
Figure 7-10b shows that an iterative computation of
F
6
computes each prior term once. The recursive
solution is clearly less efficient. The next segments will show you just how inefficient it is.
FIGURE 7-10
The computation of the Fibonacci number
F
6
using (a) recursion;
(b) iteration
F
2
is computed 5 times
F
3
is computed 3 times
F
4
is computed 2 times
F
5
is computed once
F
6
is computed once
F
6
(a)
F
5
F
4
F
4
F
3
F
3
F
2
F
3
F
2
F
2
F
1
F
2
F
1
F
1
F
0
F
2
F
1
F
1
F
0
F
1
F
0
F
1
F
0
F
1
F
0
F
0
1
(b)
F
1
1
F
2
F
1
F
0
2
F
3
F
2
F
1
3
F
4
F
3
F
2
5
F
5
F
4
F
3
8
F
6
F
5
F
4
13
7.39
The time efficiency of the algorithm
Fibonacci
.
We can investigate the efficiency of the
Fibonacci
algorithm by using a recurrence relation, as we did in Segments 7.22 through Segment 7.27. First, notice
that
F
n
requires one add operation plus the operations that
F
n
-1
and
F
n
-2
require. So if
t
(
n
) represents
the time requirement of the algorithm in computing
F
n
, we have
t
(
n
)
=
1
+
t
(
n
-
1)
+
t
(
n
-
2) for
n
≥
2
t
(1)
=
1
t
(0)
=
1
This recurrence relation looks like the recurrence for the Fibonacci numbers themselves. It should not
surprise you then that
t
(
n
) is related to the Fibonacci numbers. In fact, if you look at Figure 7-10a and
count the occurrences of the Fibonacci numbers
F
2
through
F
6
, you will discover a Fibonacci sequence.
To find a relationship between
t
(
n
) and
F
n
, let's expand
t
(
n
) for a few values of
n
:
t
(2)
=
1
+
t
(1)
+
t
(0)
=
1
+
F
1
+
F
0
=
1
+
F
2
>
F
2
t
(3)
=
1
+
t
(2)
+
t
(1)
>
1
+
F
2
+
F
1
=
1
+
F
3
>
F
3
t
(4)
=
1
+
t
(3)
+
t
(2)
>
1
+
F
3
+
F
2
=
1
+
F
4
>
F
4
We guess that
t
(
n
)
>
F
n
for
n
≥
2. Notice that
t
(0)
=
1
=
F
0
and
t
(1)
=
1
=
F
1
. These do not satisfy the
strict inequality of our guess.
We now prove that our guess is indeed fact. (You can skip the proof on your first reading.)