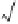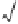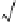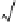Java Reference
In-Depth Information
7.40
≥
2.
Since the recurrence relation for
t
(
n
) involves two recursive
terms, we need two base cases. In the previous segment, we already showed that
t
(2)
>
F
2
and
t
(3)
>
F
3
.
Now if
t
(
n
)
>
F
n
for
n
=
2, 3, . . . ,
k
, we need to show that
t
(
k
+
1)
>
F
k
+1
. We can do this as follows:
t
(
k
+
1)
=
1
+
t
(
k
)
+
t
(
k
-
1)
>
1
+
F
k
+
F
k
-1
=
1
+
F
k
+1
>
F
k
+1
We can conclude that
t
(
n
)
>
F
n
for all
n
Proof by induction that
t
(
n
)
>
F
n
for
n
≥
2.
(
F
n
). Recall that the Big Omega
notation means that
t
(
n
) is at least as large as the Fibonacci number
F
n
. It turns out that we can compute
F
n
directly without using the recurrence relation given in Segment 7.37. It can be shown that
Fn
=
(
a
n
Since we know that
t
(
n
)
>
F
n
for all
n
≥
2, we can say that
t
(
n
)
=
Ω
b
n
)
/
−
5
b
n
where
a
=
/
2 and
b
=
/
2. Since
<
2, we have
b
and
. There-
(
15
+
)
(
15
-
)
15
-
<
1
<
1
fore, we have
Fn
>
(
a
n
−
1)
/
5
(
a
n
). Some arithmetic shows
that the previous expression for
a
equals approximately 1.6. We conclude that
t
(
n
) grows exponentially
with
n
. That is, the time required to compute
F
n
recursively increases exponentially as
n
increases.
(
a
n
), and since we know that
t
(
n
)
=
Thus,
F
n
=
Ω
Ω
(
F
n
), we have
t
(
n
)
=
Ω
7.41
At the beginning of this section, we observed that each Fibonacci number is the sum of the preced-
ing two Fibonacci numbers in the sequence. This observation should lead us to an iterative solution
that is O(
n
). (See Exercise 9 at the end of this chapter.) Although the clarity and simplicity of the
recursive solution makes it a tempting choice, it is much too inefficient to use.
Programming Tip:
Do not use a recursive solution that repeatedly solves the same
problem in its recursive calls.
Question 11
If you compute the Fibonnaci number
F
6
recursively, how many recursive
calls are made, and how many additions are performed?
Question 12
If you compute the Fibonnaci number
F
6
iteratively, how many additions
are performed?
7.42
Tail recursion
occurs when the last action performed by a recursive method is a recursive call. For
example, the following method
countDown
from Segment 7.6 is tail recursive:
public static void
countDown(
int
integer)
{
if
(integer >= 1)
{
System.out.println(integer);
countDown(integer - 1);
}
// end if
}
// end countDown
A method that implements the algorithm
Fibonacci
given in Segment 7.37 will not be tail recur-
sive, even though a recursive call
appears
last in the method. A closer look reveals that the last
action
is an addition.
The tail recursion in a method simply repeats the method's logic with changes to parameters and
variables. Thus, you can perform the same repetition by using iteration. Converting a tail-recursive
method to an iterative one is usually a straightforward process. For example, let's see how to convert