Biomedical Engineering Reference
In-Depth Information
120
100
n=0.0
n=0.1
n=0.2
n=0.3
n=0.4
n=0.5
80
C
σε
60
C
σ
40
RR
r
= 2· 0.0115
m
= 2.0
R
Elastic limit
Plastic limit
α
ε
=°
=
70.3
0.0115
20
Eq. (9)
R
Eq. (13)
0
(c)
0
1000
2000
3000
4000
E
/
σε
E
/
σ
R
R
R
Figure 6-4. The relationship between
.
The numerical results (symbols) are shown with both elastic and rigid plastic limits, and
the empirical fitting function incorporating these limits is given in
Eq. 6-13
(which can be
extended to other indenter angles).
C
/
σ
and
as
n
is varied, for
α =°
70.3
E
/
σ
R
R
For a given indenter angle
α
, once the dimensionless loading
curvature Π is determined, if both
E
and
ν
known
a priori
, the only
apparent unknown variable
σ
can be solved numerically from the
pair of flow stress-total strain (
R
) on the uniaxial stress-strain curve
can be determined from the reverse analysis as
σε
,
= = +
. (6-14)
Finally, by using the dual (or plural) sharp indenter method, more
pairs of true stress-strain can be determined from the indentation analysis
when different
α
are used. It is commonly believed that the
dimensionless loading function
Π
σσ
and
ε ε
2
2
σ
/
E
R
R
R
ε
are
sufficiently different when another
α
is used.
1,53,56,73
For power-law
materials, two independent conical indentation tests with distinct apex
angle
and representative strain
R
and
n
(assuming both
E
and
ν
are known); more indenter angles with larger
separation may be used and the averaged result improves the accuracy of
the reverse analysis.
5,74
α are ne
ed
ed to determine the plastic parameters
σ
y





































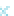


























































Search WWH ::

Custom Search