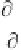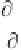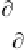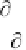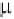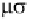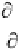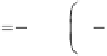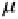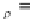Geology Reference
In-Depth Information
where
R
e
denotes the real part, then equation (3.64) can
be rewritten as
−
i
(
σ
/
ω
). This is the rationale behind the definition of
the complex dielectric constant equation (3.63). By com-
paring equations (3.63) and (3.68), it can be seen that
the real part in the definition is the permittivity and the
imaginary part is proportional to the conductivity, with
an explicit dependence on the frequency of the electro-
magnetic field. The negative sign of the imaginary part
has resulted from the second derivative of the exponential
term in equation (3.65). The solution of equation (3.68) in
cases of low‐loss, high‐loss, and general‐lossy media can
be found in
Ulaby et al.
[1986]. It suffices to mention here
that the solution for the general‐lossy media is a decaying
harmonic function, defined as
2
E
Z
X
(3.66)
E
2
The magnetic field vibration is governed by a similar
equation. The electromagnetic wave is therefore affected
by and
μ
. The former represents the capacitive prop-
erty and the latter represents the inductive property of
the material in response to an applied magnetic field.
The permeability of most materials is close to 1, which is
the value of permeability of free space. Therefore, the
electromagnetic wave propagation depends only on .
The solution to equation (3.66) is introduced in several
textbooks on electromagnetic wave theory [e.g.,
Lorrain
et al.,
1986]. It shows that both electric and magnetic vec-
tors propagate with the same velocity and phase without
attenuation. The permittivity is a real number in this case,
i.e., is equivalent to ʹ in equation (3.63). In nonideal
(lossy) dielectrics, the energy loss is manifested in the
form of conduction currents and is represented in the
wave propagation equation by a “diffusion” term (the last
term on the RHS of the following equation):
1
2
j
1
j
tan
E
Z
E e
(3.69)
X
X
0
The attenuation of this function depends on tan
δ
, which
is defined as (″/′) and is called the loss tangent. The
distance over which the amplitude of the incident radia-
tion decreases by a factor (1/
e
) is called the penetration
depth
δ
ρ
. It is related to the loss tangent by the following
equation [
Evans,
1965]:
1
2
2
42
1
1
(3.70)
2
2
E
Z
E
t
E
t
X
X
X
(3.67)
2
2
where
λ
is the wavelength of the incident radiation.
Derivation of this function is presented in section 7.3.4.
Shokr
[1998] calculated the penetration depth from
equation (3.70) using measurements of ′ and ″ for FY and
MY ice in the C‐band microwave frequency of 5.3 GHz.
Results are shown in Table 3.8. Penetration depth is
presented for three crystallographic structures of sea ice:
randomly oriented frazil, vertically oriented frazil, and
columnar ice. Definitions and illustrations of these types
are presented in section 4.3. The penetration depth in FY
where
σ
is the electric conductivity of the material. Again,
assuming harmonic time dependence of the electric field
E
X
, equation (3.66) takes the form
2
E
Z
2
X
j E
(3.68)
2
X
This form can be made equivalent to the wave equation
in an ideal dielectric if in equation (3.66) is replaced by
Table 3.8
Penetration depth in sea ice (cm) from measurements of complex dielectric constant in the microwave C‐band for
multiyear ice (melt pond and hummock) and first‐year ice (random frazil, oriented frazil and columnar ice crystalline structure).
Penetration Depth (mm) of Ice Types
Multiyear Ice
First‐Year Ice
Core
Number
Melt Pond
Hummock
Random Frazil
Oriented Frazil
Columnar Ice
1
5.07
7.58
1.61
3.55
2.49
2
5.04
7.23
1.46
2.20
2.39
3
4.25
6.06
1.33
2.28
2.54
4
4.91
7.51
2.43
2.49
5
4.66
8.38
1.98
2.22
6
4.90
7.03
2.44
7
4.36
7.01
2.86
Note
: A few ice cores from each type were used (M. Shokr, unpublished data).