Drillstring Vibrations: Classic Ideas and Modern Approaches - Wave Propagation in Drilling, Well Logging and Reservoir Applications - page 155

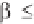
| | 1 (4.2.82)
so that the finite difference scheme is “absolutely” or “unconditionally stable.”
Numerical stability does not guarantee that a computed solution tends to a
solution of the differential equation. This issue is a subtle and important one,
and forms the subject of ongoing researches. Let us consider a practical
illustrative example for this nonconvergence. In the present case, an exact
solution u(x,t) of the differential equation is found to be
u i,n = exp[(-1) 1/2 (x i ± t n )] (4.2.83)

for real , where x i = i x and t n = n t. This is easily compared with Equation

4.2.77 if we rewrite it with = x in the form

n

U i,n = exp [(-1) 1/2 (x i ± t n )] cos (4.2.84)

where

m)} tan -1 (2m sin

= /( t) = {1/( x x /2) (4.2.85)

If x is small and is independent of x, we have by Taylor series expansion

= 1 - {(1 +8m 2 )/24}

2

x 2 + O( x 4 ) (4.2.86)

and

cos n = e x p [ n l og c os ]
= exp[(-n/2) log (1 +4m 2 sin 2 /2)]
= e x p [ - x m 2 t n /2 + O( x 3 t n )] (4.2.87)
Now, the real and imaginary parts of the exact solution oscillate
periodically in time without damping. On the other hand, the corresponding
terms of U i,n possess damped oscillations, the amplitude being attenuated like
exp [-

x m

2 t n /2 + O(

x 3 t n )] . Also, the period is increased in the ratio 1/ = 1

+ {(1 +8m 2 ) 2 x 2 /24.
Grid sizes, time steps, and convergence. All of this means that care
must be taken in judiciously selecting space and time steps. It does not imply
that numerical solution are undesirable; often, they are the only means of
obtaining solutions. From a different perspective, we must also understand that
2 u/ t 2 + u/ t - E 2 u/ x 2 + g = F e is limited as a model for the physical
system; little real benefit is obtained by solving with very fine discretization.
For example, u/ t damping, chosen for mathematical simplicity, does not
model the frequency-dependent dissipation that characterizes real drillstrings.
Practical errors in characterizing F e may exceed those associated with truncation
errors. Thus, subjective value judgments are often warranted.
Again, absolute stability is a desirable trait for numerical schemes.
However, it provides no guarantee that computations will converge to solutions
of the differential equation being modeled, even in the limit of vanishing

x and

t, if the ratio x/ t happens to be inappropriate. Convergence has long