Geology Reference
In-Depth Information
It is also important that the tridiagonal structure is “diagonally dominant,”
that is, the absolute value of the diagonal coefficient (2+1/m
2
) exceeds the sum
of the (unity) coefficients of the side diagonals. This property lends itself to
“numerical stability,” meaning that iterative solutions are not likely to “blow up”
as a result of truncation and round-off errors. This does not guarantee that the
computed solutions are correct, but it does buttress the accepted (but
questionable) philosophy that “any solution is better than no solution.”
Only two previous time levels of solution need to be stored at any given
step of the solution process, so that three levels of information are required in
total. Thus, the Fortran associated with our scheme can be written using three
dimensioned scalar arrays
UN(1000), UNM1 (1000), and UNM2(1000) only,
representing u
n
(i), u
n-1
(i) and u
n-2
(i), where the
dimension
1000 might signify
1,000 closely spaced nodes. At the end of each time step, we copy UNM1 i nto
UNM2, and UN into UNM1, and repeat the procedure until termination. It is
not necessary (or advisable) to have computer memory allocated for a complete
field U(1000,500), say, representing 1,000 nodes and 500 time steps.
Intermediate results, e.g., bit location, velocity and stress can be written to
output files for subsequent post-processing and display.
Also note that the matrix coefficients
A
,
B
, and
C
need not be recomputed
for subsequent time steps, since they are constants defined once and for all (for
example, refer to the Fortran listing in Figure 4.2.8 for matrix coefficient
definition). While the matrix solver given in Figure 4.2.6
will
destroy
A
,
B
, and
C
at the end of each inversion, thus requiring redefinition of these coefficients
prior to each integration, other solvers are available which retain their input
values but at the expense of increased memory requirements.
Stability of the scheme.
We can address the “stability” issue
quantitatively, through “von Neumann analysis.” Let us refer to Equation
4.2.70. Since the difference equation is linear, with constant coefficients, exact
solutions are sought in the “separated” form
U
i,n
=
n
exp[(-1)
1/2
i] (4.2.77)
This assumption (or, Ansatz) applies only if and are related by the equation
(1 + 4m
2
sin
2
/2)
2
- 2 + 1 = 0 (4.2.78)
a requirement found on direct substitution in Equation 4.2.70. If we now set
cos
= (1 + 4m
2
sin
2
/2)
-1/2
(4.2.79)
that is,
= tan
-1
(2m sin
/2)
(4.2.80)
it follows that
= exp[ ± (-1)
1/2
] cos
(4.2.81)
For all real values of
and m, the “amplification factor” clearly satisfies

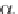

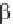
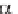

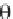













Search WWH ::

Custom Search