Information Technology Reference
In-Depth Information
2. It should be pointed out that the separation point introduced in this paper is not
the one advocated by Max Black [1]. Notice that in a, b, c, in the the figure 15.2
the Black's one is B
=
<
10
, and in figure (d) is the B
10
marked there, and that
≤
B (and s
A
≤
in all the four cases it is s
B). Hence, contrarily to what he said,
Black's point can be found in some cases, but is different from s (or s
a
) that only
classifies
[
0
,
10
]
in the two subsets of points that are
•
more P than
not
P(
opposite of
P)
less P than
not
P(
opposite of
P)
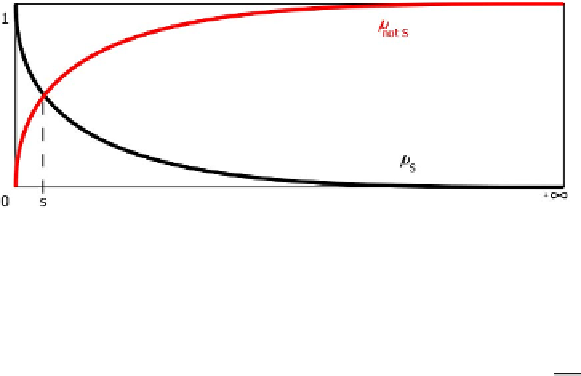
3. There are cases in which point B does not exist. For instance, if the universe is
the real semi-line
•
μ
S
tends asymptotically towards
0
(see the figure
15.3) it is clear that no point B can exist.
Nevertheless, as it appears in the figure, point s does exist.
[
0
,
+
∞
)
, and
Fig. 15.3
e
−
x
e
−
x
For instance, if it is
μ
S
(
x
)=
∈
(
0
,
1
]
, that verifies
lim
x
→
+
∞
=
0
, it follows
e
−
x
e
−
x
,ore
−
x
5
, but there is no a value B such that e
−
B
=
1
−
=
0
.
=
0
.
1
−
x
1
Provided 'not' is represented by the Sugeno's negation N
(
x
)=
x
,from
+
=
√
2
e
−
x
e
−
x
e
−
x
1
−
+
e
−
x
, it follows e
−
2
x
2
e
−
x
0
, and e
−
x
=
N
(
)=
+
−
1
=
−
1
. Hence,
√
2
1
e
−
s
2
e
−
s
1
, and s
1
<
=
−
1
<
0
.
5
=
s
2
.
4. There are also cases in which points B and s are not unique and, hence, difficult
to select. Of course, s is a supremum provided
μ
P
is decreasing, and a infimum
if
μ
P
is not monotonic, there can exist both an
infimum and a supremum. This is, for instnace, the case with A
4
μ
P
is non-decreasing. Hence, if
=
'around four'
=[
,
]
in X
μ
A
4
is non monotonic. In the figure
15.4 it is clear the existence of the infimum i
0
10
whose membership function
=
3
.
5
, and the supremum s
=
4
.
5
,
with which it is
K
1
−
id
(
μ
)=[
3
.
5
,
4
.
5
]
.
A
4
It is analogously clear that there is not a point B after which the elements in
[
0
,
1
]
are not at all around 4.
An analogous result is obtained dealing with s
a
.