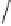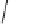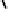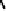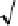Information Technology Reference
In-Depth Information
2. Find optimal step length in real and imaginary directions:
,
n
r
=
(
ck
+
2
dk
)
r
0
1
and norms
N
r
=
N
(
κ
-
n
r
ρ
),
. Square
n
i
=
(
ck
−
dk
)
r
N
=
N
(
κ
−
n
−
2
ρ
)
1
0
i
i
brackets here mean the nearest integer.
3. If
n
i
=
n
r
= 0 then set
k
← κ else
3.1. If
N
r
<
N
i
then set κ ← κ -
n
r
ρ else set
κ
←
κ
−
n
−
2
ρ
.
3.2. Go to step 2.
4. Return(
k
).
Algorithm finds representation
kk
with minimum norm
N
(
k
) <
r
and takes two iterations at most: for real and imaginary directions. In fact
this algorithm computes field isomorphism ϕ:
F
r
→
O
K
, so it gives ϕ(0) = 0, ϕ(1) = 1,
and if ϕ(
k
) = κ then ϕ(
k
+ 1) ≡ κ + 1 (mod ρ).
The process can be illustrated geometrically in complex rectangular lattice with
base vectors
≡
+
k
−
2
(mod
ρ
)
0
1
as a successive approach to the origin. It comes to a halt as
soon as quadratic integer
{
−
2
}
falls into a parallelogram, which is disposed symmetrically
within the ellipse
x
2
+ 2
y
2
=
r
and contains
r
integer lattice points and.
Algorithm can be speeded up by analogy with usual Euc
lide
an algorithm transfor-
mation to binary one. To do this, complex number ρ (in
κ
−
2
-base notation) is rep-
∑
i
resented as a vector over {-1, 0, 1} and
k
2 is represented as a vector
(…, -
K
3
, 0,
K
2
, 0, -
K
1
, 0,
K
0
). No compu
tabl
e orbit of automorphism group is known
for given point of order
r
. Note that if − generates the whole group
F
r
*
or its large
subgroup, then orbits attack described in section 1 has no advantages over points
attack even though the orbit can be efficie
ntl
y computed. So none of known algo-
rithms for ECDLP solving is faster than
=
i
O
(
r
)
elliptic curve operations.
4
Elliptic Curve with Complex Multiplication by
(1
+
−
7
)
2
This approach is also suitable for elliptic curves with complex multiplication by
2
[
]
O
be imaginary quadratic
field and its ring of integers, respectively. Ring
O
K
is Euclidean and possess unique
factorization. Prime field characteristic
p
=
c
2
+
cd
+ 2
d
2
can be linearly transformed
to
(
+
−
7
)
. Let
K
=
Q
[
−
7
]
and
=
Z
(
+
−
7
)
2
p
=
a
2
+ 7
b
2
, where
a
≡ 0
(mod 2),
b
≡ 1
(mod 2).
So
p
≡ 3
(mod 4),
#
E
(
F
p
) =
p
+ 1 ± 2
a
≡ 0 (mod 4).
−
7
5
This curve can be given by Weiersrass equation (5) with
A
=
(Jacobi
p
(
p
+
1
4
symbol) and
. For the twisted curve coefficient
B
is of
opposite sign. Complex multiplication formulas become simpler if we use equation in
another form.
B
≡
(
2
5
)(
−
7
5
(mod
p
)