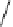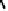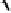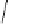Information Technology Reference
In-Depth Information
Let
in
F
p
. Complex multiplication for the curve
36
ξ
=
(
+
−
7
)
2
Y
2
Z
=
X
3
+
tX
2
Z
+
t
2
ξ
6
XZ
2
, where
t
=
−
6
(
2
+
ξ
2
)
, is given by
(
(
+
−
7
)
2
)(
X
,
Y
,
Z
)
=
(
Z
(
α
Y
2
+
X
2
),
γ
Y
(
X
2
+
δ
Z
2
),
X
2
Z
)
with
. This complex multiplication takes 8 field
multiplications, so this curve is slightly slower than the curve with complex multipli-
cation by
α
=
ξ
2
4
,
γ
=
−
ξ
3
8
,
δ
=
−
ξ
6
36
.
Complex multiplication by
−
2
.
Two successive complex multiplications by conjugates give doubling, so radix can be
represented by t
w
o or four digits from the set {-1, 0, 1}.
Let
(
−
−
7
)
2
is given by conjugate coefficients
α
,
γ
,
δ
η and η be operators of complex multiplication by conjugates. Then
2
2
r
=
a
′
ba
presents factorization of prime group
order in
O
K
. Either ρ or ρ corresponds to 0 modulo
r
. Without loss of generality we
can take ρ ≡ 0 (mod
r
). Fields
F
r
and
+
a
′
b
′ + 2
b
′
=
(
+
η
)(
a
+
b
η
)
=
ρ
O
ρ
O
consist of
r
elements and hence are
K
K
isomorphic. Isomorphism
F
r
→
can be computed by algorithm, similar to
one described in the previous section. Note that algorithm takes two iterations if it
uses orthogonal directions, that correspond to 1 and
O
ρ
O
K
K
−
7
. More iterations can occur
if non-orthogonal directions 1 and
are used.
It can be also sho
w
n that each
k
∈
F
r
can be represented as polynomial of alternat-
ing operators η and η of degree ≤ log
2
r
with {-1, 0, 1} coefficients. So using radix 4
allows speeding up elliptic curve point multiplication about 1.5 times with respect to
analogue radix 16 method.
One can use complex multiplication by
(
+
−
7
)
2
, given by isogeny of
degree 3, but formulas for complex multiplication, given by isogenies of degree ≥ 3,
are more complex than considered ones.
Elliptic curve cannot possess two or more complex multiplications in different
imaginary quadratic fields
−
3
,
(
+
−
11
)
2
−
Q
, where
D
1
,
D
2
are square-free. If
this were the case, there would be two representations
Q
[
−
D
]
,
[
D
]
2
2
2
1
p
=
a
+
f
D
b
(or
1
1
2
2
2
f
D
+
1
b
f
D
+
1
b
2
2
1
2
2
2
2
2
2
2
2
p
=
a
+
ab
+
1
1
) and
p
=
a
+
f
D
b
(or
p
=
a
+
ab
+
2
)
1
2
2
4
4
with conductors
f
1
,
f
2
[9]; this leads to contradiction.
Hence, considered elliptic curves seem to be the fastest over prime finite fields.
This arithmetic can be used also for elliptic curves in any other normal form (Legen-
dre, Hesse, etc.).