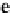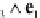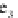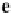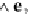Graphics Reference
In-Depth Information
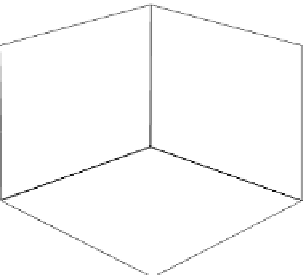
Fig. 6.3
The 3D bivectors
aligns with
e
2
,the
y
-axis, and the middle finger aligns with
e
3
,the
z
-axis. We begin
with two 3D vectors:
a
=
a
1
e
1
+
a
2
e
2
+
a
3
e
3
b
=
b
1
e
1
+
b
2
e
2
+
b
3
e
3
and their inner product is
a
·
b
=
(a
1
e
1
+
a
2
e
2
+
a
3
e
3
)
·
(b
1
e
1
+
b
2
e
2
+
b
3
e
3
)
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
and their outer product is
a
∧
b
=
(a
1
e
1
+
a
2
e
2
+
a
3
e
3
)
∧
(b
1
e
1
+
b
2
e
2
+
b
3
e
3
)
=
a
1
b
2
e
1
∧
e
2
+
a
1
b
3
e
1
∧
e
3
+
a
2
b
1
e
2
∧
e
1
+
a
2
b
3
e
2
∧
e
3
+
a
3
b
1
e
3
∧
e
1
+
a
3
b
2
e
3
∧
e
2
=
(a
1
b
2
−
a
2
b
1
)
e
1
∧
e
2
+
(a
2
b
3
−
a
3
b
2
)
e
2
∧
e
3
+
(a
3
b
1
−
a
1
b
3
)
e
3
∧
e
1
.
(6.8)
This time we have three unit basis bivectors:
e
1
∧
e
1
, and three asso-
ciated scalar multipliers:
(a
1
b
2
−
a
2
b
1
)
,
(a
2
b
3
−
a
3
b
2
)
,
(a
3
b
1
−
a
1
b
3
)
respectively.
These bivectors are the basis for a right-handed oriented axial system.
Continuing with the idea described in the previous section, the three bivectors
represent the three planes containing the respective vectors as shown in Fig.
6.3
, and
the scalar multipliers are projections of the area of the vector parallelogram onto the
three bivectors as shown in Fig.
6.4
. Note that this is the accepted definition for a
right-handed space. The orientation of the vectors
a
and
b
determine whether the
projected areas are positive or negative.
Equation (
6.8
) should look familiar as it looks similar to the cross product
a
e
2
,
e
2
∧
e
3
,
e
3
∧
×
b
:
a
1
b
3
)
e
2
.
(6.9)
This similarity is no accident, for when Hamilton invented quaternions he did not
recognise the possibility of bivectors, and invented some rules which eventually
a
×
b
=
(a
1
b
2
−
a
2
b
1
)
e
3
+
(a
2
b
3
−
a
3
b
2
)
e
1
+
(a
3
b
1
−