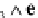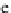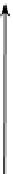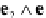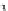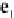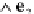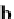Graphics Reference
In-Depth Information
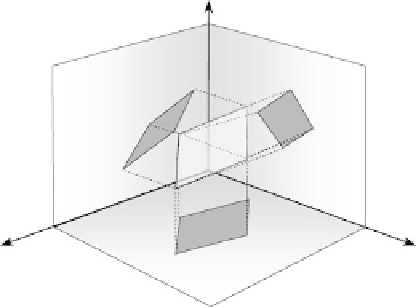
Fig. 6.4
The projections on
the three bivectors
became the vector product. In fact, we show later that quaternions are bivectors in
disguise. We can see that a simple relationship exists between (
6.8
) and (
6.9
):
e
1
∧
e
2
and
e
3
e
2
∧
e
3
and
e
1
e
1
and
e
2
.
The wedge product bivectors are perpendicular to the vector components of the cross
product. So the wedge product is just another way of representing the cross product.
However, the wedge product introduces a very important bonus - it works in space
of any dimension; whereas, the cross product is only comfortable in 3D. Not only
that, the wedge (outer) product is a product that creates volumes, hypervolumes, and
can also be applied to vectors, bivectors, trivectors, etc.
e
3
∧
6.8 The Outer Product of Three 3D Vectors
Having seen that the outer product of two 3D vectors is represented by areal pro-
jections onto the three basis bivectors, let's compute the outer product of three 3D
vectors:
a
=
a
1
e
1
+
a
2
e
2
+
a
3
e
3
b
=
b
1
e
1
+
b
2
e
2
+
b
3
e
3
c
=
c
1
e
1
+
c
2
e
2
+
c
3
e
3
a
∧
b
∧
c
=
(a
1
e
1
+
a
2
e
2
+
a
3
e
3
)
∧
(b
1
e
1
+
b
2
e
2
+
b
3
e
3
)
∧
(c
1
e
1
+
c
2
e
2
+
c
3
e
3
)
=
((a
1
b
2
−
a
2
b
1
)
e
1
∧
e
2
+
(a
2
b
3
−
a
3
b
2
)
e
2
∧
e
3
+
(a
3
b
1
−
a
1
b
3
)
e
3
∧
e
1
)
c
3
e
3
).
At this stage we introduce another axiom: the outer product is associative. This
means that
a
∧
(c
1
e
1
+
c
2
e
2
+
∧
(
b
∧
c
)
=
(
a
∧
b
)
∧
c
. Therefore, knowing that
a
∧
a
=
0: