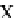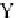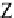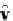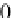Graphics Reference
In-Depth Information
Fig. 11.7
The point
(
1
,
0
,
0
)
is rotated 180° about the
vector
v
to
(
0
,
0
,
1
)
which not only looks like a rotation matrix, but has a determinant of 1 and rotates
the point
(
1
,
0
,
0
)
to
(
0
,
0
,
1
)
as shown in Fig.
11.7
,
⎡
⎤
⎡
⎤
⎡
⎤
0
0
1
001
0
1
0
0
⎣
⎦
=
⎣
⎦
⎣
⎦
.
10
100
−
11.4 Multiple Rotations
Say a vector or frame of reference is subjected to two rotations specified by
q
1
followed by
q
2
. There is a temptation to convert both quaternions to their respective
matrix and multiply the matrices together. However, this not the most efficient way
of combining the rotations. It is best to accumulate the rotations as quaternions and
then convert to matrix notation, if required.
To illustrate this, consider the vector
p
subjected to the first quaternion
q
1
:
q
1
pq
−
1
1
followed by a second quaternion
q
2
q
2
q
1
pq
−
1
q
−
1
2
1
which can be expressed as
(
q
2
q
1
)
p
(
q
2
q
1
)
−
1
.
Extra quaternions can be added accordingly. Let's illustrate this with an example.
To keep things simple, the first quaternion
q
1
rotates 30° about the
y
-axis:
q
1
=
cos 15°
+
sin 15°
j
.
The second quaternion
q
2
rotates 60° also about the
y
-axis:
q
1
=
cos 30°
+
sin 30°
j
.
Together, the two quaternions rotate 90° about the
y
-axis. To accumulate these ro-
tations, we must multiply them together: