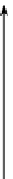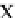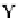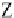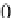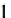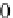Graphics Reference
In-Depth Information
Fig. 11.6
The point
P(
0
,
1
,
1
)
is rotated 90° to
P
(
1
,
1
,
0
)
about the
y
-axis
Substituting these values in (
11.3
)gives
⎡
⎤
⎡
⎤
⎡
⎤
1
1
0
001
010
−
0
1
1
⎣
⎦
=
⎣
⎦
⎣
⎦
100
where
(
0
,
1
,
1
)
is rotated to
(
1
,
1
,
0
)
, which is correct.
So now we have a transform that rotates a point about an arbitrary axis intersect-
ing the origin without the problems of gimbal lock associated with Euler transforms.
Before moving on, let's evaluate one more example. Let's perform a 180° ro-
tation about a vector
v
=
+
k
passing through the origin. To begin with, we will
deliberately forget to convert the vector into a unit vector, just to see what happens
to the final matrix. The quaternion should take the form
i
=
+
ˆ
q
cos
(θ/
2
)
sin
(θ/
2
)
v
but we will use
v
as specified. Therefore, with
θ
=
180°
s
=
0
,x
=
1
,y
=
0
,z
=
1
.
Substituting these values in (
11.3
)gives
⎡
⎤
102
0
⎣
⎦
10
201
−
which looks nothing like a rotation matrix, and reminds us how important it is to
have a unit vector to
re
present
t
he axis. Let's repeat these calculations normalising
the vector to
i
/
√
2
k
/
√
2:
ˆ
+
v
=
1
√
2
1
√
2
s
=
0
,x
=
,y
=
0
,z
=
.
Substituting these values in (
11.3
)gives
⎡
⎤
⎦
001
0
⎣
10
100
−