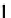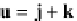Graphics Reference
In-Depth Information
Fig. 11.5
The point
P(
0
,
1
,
1
)
is rotated 90° to
P
(
1
,
1
,
0
)
about the
y
-axis
qpq
−
1
=
(
1
−
cos
θ)(
v
ˆ
·
u
)
ˆ
v
+
cos
θ
u
+
sin
θ
v
ˆ
×
u
=
j
·
(
j
+
k
)
j
+
j
×
(
j
+
k
)
j
and confirms that
P
is indeed rotated to
(
1
,
1
,
0
)
.
Before moving onto the next section it is worth clarifying the interpretation of the
two triples described above. As with the rotation transforms previously covered, we
have used
R
θ,
v
to describe a point rotation,
θ
about the vector
v
, and
R
−
1
=
i
+
θ,
v
to describe
a frame rotation
θ
about the vector
v
. Therefore, in keeping with this convention, we
will use
qpq
−
1
to describe a point rotation of the point represented by
p
about the
quaternion's vector. And
q
−
1
pq
to describe a frame rotation about the same vector.
11.3 Quaternions in Matrix Form
Having discovered a vector equation to represent the triple
qpq
−
1
, let's continue
and convert it into a matrix. We will explore two methods: the first is a simple vec-
torial method which translates the vector equation representing
qpq
−
1
directly into
a matrix form; the second method uses matrix algebra to develop a rather cunning
solution. Let's start with the vectorial approach, for which it is convenient to de-
scribe the unit quaternion as
q
=
s
+
v
=
s
+
x
i
+
y
j
+
z
k
and the pure quaternion as
p
=
0
+
u
which means that the triple becomes
qpq
−
1
+
s
2
2
u
u
.
And as we are working with unit quaternions to prevent scaling
s
2
=
2
(
v
·
u
)
v
−|
v
|
+
2
s
v
×
2
+|
v
|
=
1