Biology Reference
In-Depth Information
and above treatment 1 and
t
i
's correspond to the individual physician
effects.
This problem belongs to the class of problems considered by
Neyman and Scott (1948). Suppose we use invariance to eliminate the
nuisance parameters
t
i
's corresponding to the physician effect. Notice
that
X
i,
2
X
i
,1
is a maximal invariant under the group of translations
and
X
i,
2
X
i
,1
~
N
((
1
),2)
. Similarly
Y
j,
2
Y
j
,1
~
N
((
1
)
(
1
),2
.
2
2
2
Let us denote
d
. Now consider the partition
d
,(
1
)
2
1
2
R
2
,
R
2
}
induced by
of the original parameter space
{(
,
,
):
this maximal invariant:
such that
Orbit
(
d
,
d
)
{(
,
)
d
}.
Now consider the likelihood for two sets of parameters,
(
d
,(
1
)
2
1
2
*
)
and
where , that is, they
belong to the same orbit induced by the maximal invariant. Since the
distribution of the maximal invariant is a function of
(
d
,d
)
, it is clear
that the two combinations of the parameters have identical likelihood.
An immediate consequence of this is that
1
and
2
, the change in the
diastolic blood pressure and the change in the systolic blood pressure,
are not identifiable. We can only find out if the change in the diastolic
blood pressure is larger or smaller than the change in the systolic
blood pressure and the magnitude of that difference. But the question:
How much does the treatment 2 reduce systolic blood pressure or dias-
tolic blood pressure, is unanswerable in this situation.
Instead of accepting this limitation of the data, we decide to follow
the superimposition logic and conduct the following analysis.
*
,
1.
Least squares approach:
Since there are nuisance parame-
ters related to the translation group, we first superimpose, that
is translate, the observations in Sample 1 in such a manner
that is minimized. This corre-
sponds to transforming the observations
to Similarly, we translate the observations
in Sample 2 to Now, we average these trans-
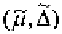
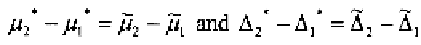
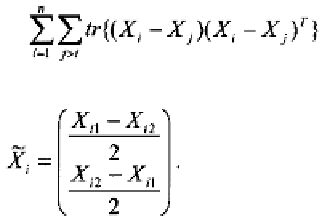
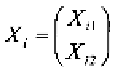
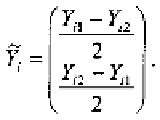
Search WWH ::

Custom Search