Biology Reference
In-Depth Information
We say that these two transformations are equivalent to each other.
Let us denote by
H
M
1
,M
2
, the set of transformations that map an ele-
ment of the orbit of
M
1
to an element of the orbit of
M
2
.
The key result that follows from the maximal invariance machinery
developed in
Chapter 3
,
Part 2
, is that:
For
h
1
,
h
2
Data
)
.
That is, data cannot help us distinguish between the transforma-
tions that map an element of the orbit of
M
1
to an element of the orbit
of
M
2
. It is thus imperative that our inferences be invariant to the
choice of a particular transformation within
H
M
1
,M
2
. This is precisely
the requirement specified in definition 1.
It seems, however, that the superimposition and deformation meth-
ods are able to specify a particular transformation from this class. How
is that possible? The superimposition methods choose one of the trans-
formations
H
M
1
,M
2
using an external criterion such as the least squares.
Similarly the thin-plate splines methods choose a particular transfor-
mation that minimizes the bending energy or some such external
criterion.
No amount of data can instruct us which of these external cri-
terion is valid in nature.
We have shown in
Part 1
of this chapter that
the inferences based on these different criteria can be quite distinct
from each other. Our argument is that since data cannot distinguish
between these different criteria and hence these different scientific
inferences, the proper thing to do is to base statistical and scientific
inferences
only
on those quantities that remain invariant to the choice
of a particular transformation in
H
M
1
,M
2
.
To argue that this may be problematic, we consider a somewhat
simpler situation where the issues are transparent. Suppose we are
studying two treatments for reducing blood pressure. Suppose we have
several physicians in the study. Each physician selects one of his
patients and administers one of the treatments. After a month, reduc-
tion in the blood pressure is reported as reduction in diastolic and
systolic blood pressure.
Let
X
1
,
X
2
,…,
X
n
denote the observations under the first treatment
and
Y
1
,
Y
2
,…,
Y
m
denote the observations under the second treatment.
Suppose we model these data as:
X
i
~
N
(
H
M
1
,M
2
,
likelihood
(
h
1
Data
)
likelihood
(
h
2
1
t
i
,
I
)
and
Y
j
~
N
(
1
t
j
,
I
)
where is the mean reduction in the diastolic and systolic blood
pressure due to treatment 1,
is the effect of treatment 2 over
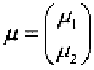


Search WWH ::

Custom Search