Biology Reference
In-Depth Information
orbits are chosen to evaluate the affine deformation. However, if one is
interested in the singular values of the affine deformation matrix
A
,
then it is clear that singular values are invariant. Thus, the measure
of anisotropy, defined as the logarithm of the ratio of the singular val-
ues (Small, 1996, page 95), is invariant.
The affine deformation is the simplest type of deformation function.
In practice, more complex types of deformation functions are required.
For example, Bookstein (1989, 1991, and 1996) suggests the use of thin
plate splines as a deformation function. An advantage of thin plate
splines is that it depicts the deformation geometrically and that the
total deformation can be decomposed into several orthogonal compo-
nents which, in turn, can be studied in order to localize the form
differences. Such localization, presumably, helps understand the bio-
logical processes that might be responsible for the form change. We
refer the reader to Bookstein's work for more details and applications.
We would also like to point out that deformation functions other than
the thin-plate splines may also be used.
We now consider the non-invariance of the thin plate splines in
more detail. Assume that the objects under consideration are two-
dimensional. Let
d
ij
denote the Euclidean distance between landmarks
i
and
j
in
M
1
, and let
U
(
d
)
d
2
log
d
2
. Let
U
be a
K
K
matrix given by
U
[
U
(
d
ij
)]
i,j=
1
,
2
,…,K
. According to the thin plate splines model, the rela-
tionship between the two forms is given by:
M
2
1
t
T
UN
where
t
is the translation parameter,
A
is a 2 x 2 matrix corresponding to the
affine deformation, and
N
is a
K
M
1
A
2
matrix corresponding to the non-
affine deformation parameters. Notice that there are
(2
K
2)
unknown parameters whereas the system of equations given by
M
2
1
t
4
UN
has only
2
K
equations. In order to make the parameters
identifiable, one needs additional constraints. Traditionally, in the
thin-plate splines literature (e.g.,Cressie, 1991, page 181), additional
constraints are imposed by presuming that the parameter
N
is such
M
1
A
that The resultant thin-spline function is termed as the
'minimum bending energy' spline.
There are, of course, any number of different external constraints
that may be considered to make the parameters identifiable. A class of
such constraints that is considered in practice (Rohlf, 1996) can be
described as follows. Let and
W
be any
K
K
symmetric

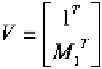
Search WWH ::

Custom Search