Biology Reference
In-Depth Information
which members of the two orbits, corresponding to
M
1
and
M
2
, are cho-
sen to calculate the form difference. One should be able to take any
member of the first orbit, any member of the second orbit, and calcu-
late a form difference that is invariant to the choice of the particular
members.
There are several different measures of form difference that are
used in practice. We examine some of the prominent ones in light of the
above definition.
4.14 Deformation approach to form difference
Let
M
1
and
M
2
be two mean forms under consideration. A typical way
to represent the relationship between
M
1
and
M
2
is to consider
M
1
being deformed into
M
2
by a function
h
. Typically a parametric family
of functions represents this deformation. Thus we have
M
2
=
h
(
M
1
,
/
)
and the value of the parameter
/
helps us understand the underlying
biological mechanisms that are associated with this deformation.
To make the basic ideas understandable, let us consider the simplest
case of two-dimensional objects with three landmarks each. We assume
that the only possible deformation is of the simplest type — an affine
deformation. Under this model,
M
2
1
t
T
where
A
is any 2 x 2
matrix and
t
is a translation vector. Thus the parameter of interest is
A
and
t
is the nuisance parameter. It is easy to see that
A
M
1
A
(
LM
1
)
-1
(
LM
2
)
where
L
is the translation matrix defined in
Chapter 3
.A physical inter-
pretation can be given to this matrix
A
by writing its singular value
decomposition in the following manner (Goodall and Green, 1986):
The angle
-
corresponds to the initial rotation to the principal axes
of
M
1
, the singular values
p
and
q
correspond to the stretching along
the principal axes and the angle
corresponds to the rotation of the
deformed
M
1
to match exactly with
M
2
. From the scientific point of
view, the parameters of interest are (
-
,
p
,
q
) because they contribute to
the deformation, whereas the parameter
does not. Let us examine
whether
A
is invariant as a measure of form difference. In the notation
used in definition 1,
Diff
(
M
1
,
M
2
)
(
LM
1
)
-1
(
LM
2
)
, whereas,
Diff
(
M
1
R
1
A
R
1
-1
Diff
(
M
1
,
M
2
)
R
2
. Thus, this measure
of form difference is not invariant. It depends on which members of the
1
t
1
T
,
M
2
,
R
2
1
t
2
T
)
R
1
-1
AR
2
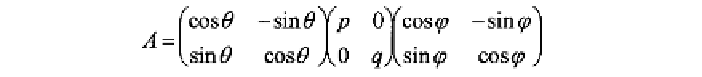
Search WWH ::

Custom Search