Biology Reference
In-Depth Information
The following expressions provide the first two moments of the ran-
dom matrix
Y
(Alam and Mitra, 1990).
D
å
2
j
j
+
s
mn
d
lp
j
+
s
mp
d
l
j
}
Cov
(
Y
lm
,
Y
np
)
=
{
s
ln
s
mp
+
s
lp
s
mn
+
s
ln
d
mp
+
s
lp
d
mn
j
=
1
Without loss of generality, one can assume
1
1
. Notice that there
1)/2
unknowns. We choose as many moments and
equate the sample moments with the corresponding population
moments. Solving the resultant equations, one can numerically obtain
the estimates of the parameters
(
are
(
KD
1)
K
(
K
*
K
,
D
)
. Given
these estimates, we obtain the mean form of the object (up to transla-
tion, rotation and reflection). From the definition of
j
's, it is clear that
they are symmetric matrices with rank 1. One can write
j
2
,…,
D
,
1
,
2
,…,
d
j
d
j
T
,
where
d
j
is a scaled eigenvector. If the observations are coming from
two-dimensional objects, the estimate of the mean form up to transla-
é
0
0
ù
ˆ
M
=
tion, rotation, and reflection is given by
ê
ú
˙
,
l
2
d
1
d
2
ë
û
whereas for three-dimensional objects, the estimate of the mean form
up to translation, rotation and reflection is given by
é
0
0
0
ù
M
=
ê
ú
˙
.
d
1
ˆ
d
2
ˆ
d
3
l
2
l
3
ë
û
Estimation of the variability around landmarks
In many important biological problems, it is of interest to know the
variability around each of the landmarks individually. So far the
results described above suggest that it is possible to estimate
L
K
L
T
but not
K
itself. However, if one is willing to assume a somewhat sim-
pler structure for
K
and
D
, then it is possible to estimate the
variability around each of the landmarks. We assume that the land-
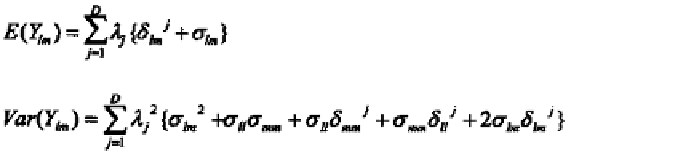









Search WWH ::

Custom Search