Biology Reference
In-Depth Information
Estimating the covariance matrix
K
*
Having obtained the estimator of the mean form matrix
M
described
above, it is fairly simple to obtain the estimator of the covariance
K
*
.
Notice that
Y
(
LX
)(
LX
)
T
~Wishart
((
LM
)(
LM
)
T
,
L
K
L
T
)
with
D
degrees of
freedom.
The mean of the non-central Wishart distribution is given by
(Arnold, 1981)
E
(
Y
)
(
LM
)(
LM
)
T
K
L
T
)
. Hence, the moment estima-
D
(
L
tor of
K
*
K
L
T
is given by:
L
where
M
is the estimator of the mean form as obtained at the end of
Step 4.
The estimator of
K
*
obtained above, although square and symmet-
ric, is not guaranteed to be positive semi-definite. One can obtain a
positive semi-definite version using a procedure, sometimes known as
Principal Coordinate Analysis. Consider the spectral decomposition of
the matrix
K
*
, namely,
ˆ
ˆ
PDP
T
where matrix
D
is a diagonal
matrix with the diagonal elements corresponding to the eigenvalues of
K
*
. Replace the negative elements in
D
by zero and call this modified
matrix
~
D
. Obtain a new matrix
ˆ
K
*
P
~
DP
T
. This matrix is guaranteed
to be square, symmetric, and positive semi-definite.
The estimator given above is slightly different than the one
described in Lele (1993). In that paper, instead of
L
K
*
K
L
T
, an estimator
for
H
K
H
T
was provided. In this monograph, we use the centering
matrix
L
, instead of
H
, to remain consistent with the rest of the chap-
ter. Replacing
L
in the above description by
H
retrieves the formulae
and description in Lele (1993).
In the above discussion, we assumed that
D
I
. This imposes some
restrictions on the applicability of this model. We now consider a more
general situation where the covariance structure is given by
K
D
.
For notational simplicity, let
Y
LX
(
LX
)
T
. Let
Y
[
Y
lm
]
where
T
(
X
)
1,2,…,
K
denoting the individual elements of the
matrix
Y
. From the previous section, we know that
Y
is distributed as
a linear combination of non-central Wishart random variables with
parameters given by
(
l
1,2,…,
K
;
m
K
L
T
,
D
D
)
.
Let
D
L
1
1
,
2
2
,…,
K
*
lm
j
]
. It follows from their definition that the
matrices
j
's are symmetric and that
lm
]
and
j
[
[
d
l
j
=
d
l
j
j
.
d
mm


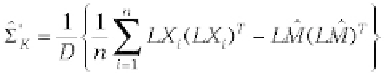


Search WWH ::

Custom Search