Information Technology Reference
In-Depth Information
g
8
g
7
g
5
g
4
g
6
x
3
x
1
x
2
x
4
Figure 9.4
A circuit in which gates
g
4
has maximal distance from the output gate
g
8
.Theinput
x
2
has fan-out 2.
values for the four assignments to inputs,
f
has at most two subfunctions, contradicting the
definition of
f
.
If
n
=
3, this fact demonstrates that the fan-out from the three inputs has to be at
least 4, that is, the circuit has at least four inputs. From Theorem
9.3.1
it follows that
C
Ω
(
f
)
3for
n
=
3. This is the base case for a proof by induction.
The inductive hypothesis is that for any
f
∗
∈
≥
2
n
−
Q
(
n−
1
)
2,3
,
C
Ω
(
f
∗
)
≥
2
(
n
−
1
)
−
3. From
Q
(
n
)
the earlier argument it follows that there is an input vertex
x
i
in a circuit for
f
∈
2,3
that
has fan-out 2. Let
x
i
have that value that causes the subfunction
f
∗
of
f
to be in
Q
(
n−
1
)
2,3
.
Fixing
x
i
eliminates at least two gates in the circuit for
f
because each gate connected to
x
i
either has a constant output, computes the identity, or computes the
NOT
of its input. The
negation, if any, can be absorbed by the gate that precedes or follows it. Thus,
C
Ω
(
f
∗
)+
2
C
Ω
(
f
)
≥
≥
2
(
n
−
1
)
−
3
+
2
=
2
n
−
3
which establishes the result.
As a consequence of this theorem, the function
f
(
n
)
mod
3,
c
requires at least 2
n
−
3 gates over
the basis
B
2
. It can also be shown to require at most 3
n
+
O
(
1
)
gates [
86
].
We now derive a second lower-bound result using the gate-elimination method. In this
case we demonstrate that the upper bound on the complexity of the m
ulti
plexer function
f
(
n
)
introduced in S
ect
ion
2.5.5
,whichis2
n
+
1
+
O
(
n
√
2
n
)
, is optimal to
2
n
+
n
mux
:
B
→B
within an additive term of size
O
(
n
√
2
n
)
. (The multiplexer function is also called the
storage
access function
.) We generalize the storage access function
f
(
n
,
k
)
SA
n
+
k
:
B
→B
slightly and
write it in terms of a
k
-bit address
a
and an
n
-tuple
x
, as shown below, where
|
a
|
denotes the
integer represented by the binary number
a
and 2
k
≥
n
.:
f
(
n
,
k
)
SA
(
a
k−
1
,
...
,
a
1
,
a
0
,
x
n−
1
,
...
,
x
0
)=
x
|
a
|
mux
=
f
(
2
m
,
m
)
Thus,
f
(
m
)
SA
.
To derive a lower bound on the circuit size of
f
(
n
,
k
)
SA
we introduce the class
F
(
n
,
k
)
of
s
Boolean functions on
n
+
k
variables defined below.


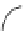
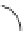








































Search WWH ::

Custom Search