Mathematical Morphology and Rough Sets - Rough Fuzzy Image Analysis: Foundations and Methodologies - page 73

(4.3a) Two overlapped sets with
tolerance relation

(4.3b) Two disjoint set with tol-
erance relation

(4.3c) Inclusion and tolerance
relation

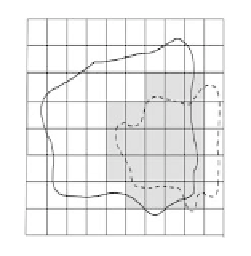
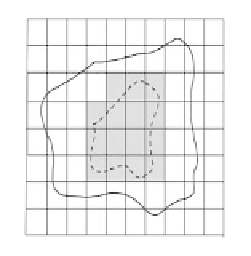
FIGURE 4.3: Tolerance relation between sets; Space X is partitioned into squares, Sets
A(solid line), set Y dashed lines have tolerance relation. A∩Y are colored in gray

The relation ∼ = X,ϕ,ε is a special case of the tolerance near set relation ∼ = B,ε (Peters, 2009)
(see, also, the weak nearness relation in (Peters and Wasilewski, 2009)). For conciseness, ∼ =
is used to denote ∼ = X,ϕ,ε . In a manner similar to what L. Polkowski has done in defining the
equivalence class of a rough set A⊂X, we introduce the following equation as a tolerance
class for a rough subset of the universe, A⊂X, with A 6= A:

A / ∼ ={Y⊆U|A∩Y 6= φ}. (4.22)

=

In other words we are suggesting that two rough sets of universe A, Y⊂X have tolerance
relation( ∼ = ) with each other iff A∩Y 6= φ. Notice that equation 4.21 is defined on elements
in a set X. By contrast, equation 4.22 is defined for two sets.

Proposition 4.4.1 ∼ = is a tolerance relation.

Proof. To show ∼ = is a tolerance relation, we have to show that it is reflexive and symmetric:
•if A = Y⇒A = Y therefore A∩Y 6= φ; So A ∼ = Y . This means that ∼ = is a
reflexive relation, A ∼ = A.
•if A ∼ = Y⇒A∩Y 6= φ⇒Y∩A 6= φ⇒Y ∼ = Y ; therefore ∼ = is a symmetric
relation.

€

Proposition 4.4.2 Equation4.20 is the specialization of equation 4.22.

Proof. We have to show that the equivalence class of a set A is a special case of its toler-
ance class. In other words, an equivalence class A /∼ is included in A / ∼ . Let Y⊂X and

=

. Since Y∈A /∼ , we have A = Y and A = Y .
We only need the first part; by A = Y we get A∩Y = A 6= φ. Therefore A /∼ is included
in A / ∼

Y∈A /∼ , we have to show that Y∈A / ∼

=

. €

=

Figure 4.3 are showing three different sets that have tolerance relation with set A⊂X. In
figure 4.3b the set Y⊂X is disjoint from the set A with A∩Y = φ, but has a tolerance
relation with A because A∩Y 6= φ.