Mathematical Morphology and Rough Sets - Rough Fuzzy Image Analysis: Foundations and Methodologies - page 72

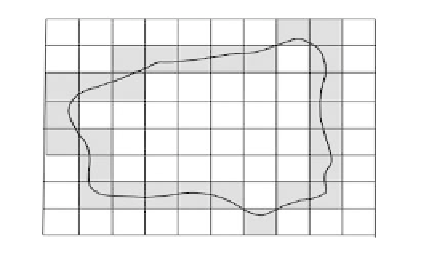
(4.2a) Set A in the partitioned space X, where the
boundary region contains shaded rectangles

(4.2b) Sets A (solid line) and Y (dashed line) have
equivalence relation with each other

FIGURE 4.2: Equivalence relation between sets

Polkowski(Polkowski, 1993), also defined an equivalence relation based on topological prop-
erties of rough set. For a rough subset of universe, A⊂X, with

A 6= A, the equivalence

class A /∼ is defined as:

A /∼ ={Y⊆X|A = Y

and A = Y}. (4.20)

In other words, the equivalence class of a set X is the collection of those sets with the
same interior and closure of a set X. Notice that in equation 4.14, an equivalence class is
based on an element x∈X, whereas, in equation 4.20, an equivalence class of a set A⊆X
is calculated. Figure 4.2 demonstrates the idea of sets that have an equivalence relation
with each other. Those rough sets with equal interior and closure have an equivalence
relation with each other. In other words, all those sets that fall into boundary regions of
the set X have an equivalence relation with A. Figure4.2b shows the boundary region of
a set A (solid line), and a sample set Y (dashed line) that has an equivalence relation with A.

Instead of using an equivalence relation, arbitrary binary relations can be used to form an
approximation space that is called a generalized approximation space. In this case, instead
of having partitions on X, a covering can be defined by a tolerance relation. That is, if we
use the tolerance relation ∼ = X,ϕ,ε defined in (4.21) instead of equivalence relation∼, ∼ = X,ϕ,ε
defines a covering on X, i.e., the tolerance classes in the covering may or may not disjoint
sets. The result from A. Skowron and J. Stepaniuk is called a tolerance approximation
space (Skowron and Stepaniuk, 1996). E.C. Zeeman formally defined a tolerance relation ∼ =
on a set X as a reflexive and symmetric relation and introduced the notion of a tolerance
space (Zeeman, 1962) ∗ . A special kind of tolerance relation is a well known equivalence
relation, which is reflexive, symmetric and transitive and is similar to equation 4.13. For
example, we can define a tolerance relation on the set X as given in (4.21).

∼ = X,ϕ,ε ={(x, y)∈X×X :|ϕ(x)−ϕ(y)|≤ }.

(4.21)

∗ It has been observed by A.B. Sossinsky (Sossinsky, 1986) that it was J.H. Poincare who informally
introduced tolerance spaces in the context of sets of similar sensations (Poincare, 1913). Both E.Z.

Zeeman and J.H. Poincare introduce tolerance spaces in the context of sensory experience.