PerformingTemplate-Based Reconstruction - Deformable Surface 3D Reconstruction from Monocular Images - page 44

Image Image

u

v v'

v'

w' w

v

w

( (

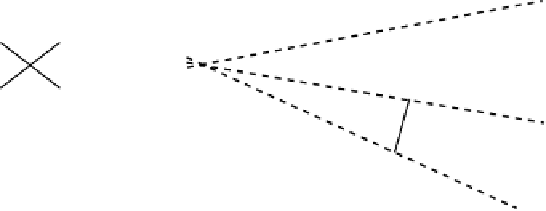
Figure 4.14: (a) Under orthographic projection, even when the average depth and length of a segment
are known, the location of its 3D points is only determined up to a front to back reversal ambiguity. (b)
Under perspective projection, knowing the length of a segment can be used to establish upper bounds
on the depth of its points. Note that, for a point belonging to two segments, several disagreeing upper
bounds can be obtained.

where is the set of mesh edges. These constraints are quadratic in the v i , and thus in the β i , but not

convex. Furthermore, there are typically many of them—several thousands in the case of the mesh
of Fig. 4.8 —since there is one per edge of the mesh. As in Moreno-Noguer et al. [ 2009 ], extended
linearization Courtois et al. [ 2000 ] is used to solve the resulting large quadratic system in terms
of the β i , from which the shape can then be computed. In Salzmann and Fua [ 2011 ], it was first
suggested to exploit the same Euclidean distance constraints as in Salzmann et al. [ 2008a ], and to
rely on the same extended linearization technique, but using a local deformation model. In practice,
however, using local instead of global models in this way does not significantly change the results as
the surface is effectively prevented from developing sharp creases by the constraints.
Approaches to exploiting inextensibility constraints by considering distances between in-
terest points on the surface instead of between mesh vertices have also been proposed. The one
of Ecker et al. [ 2008 ] relies on the fact that, under orthographic projection, preserving the distance
between two points constrains the segment linking them up to a potential front to back reversal, illus-
trated by Fig. 4.14 (a). Reconstructing these segments whose orientation presents a binary ambiguity
and regularizing them with a spline-based smoothness term amounts to solving a Semi Definite
Programming problem, for which effective software tools exist Sturm [ 1999 ]. A similar philosophy
is pursued in Perriollat et al. [ 2010 ] but in the full projective case. In that situation, forcing the
distance between two feature points to remain constant can be used to establish upper bounds on
their depth, as shown in Fig. 4.14 (b). The surface reconstruction process starts by computing these
bounds for all pairs of neighboring points, and iteratively refines them to make them consistent with
each other. The resulting point cloud can be taken as the final solution, or can be smoothed by fitting
a thin-plate spline to it. A strength of these approaches as compared to Salzmann et al. [ 2008a ]is
that, initially at least, no assumptions need be made about surface smoothness.

E