Image Processing Reference
In-Depth Information
(a)
(b)
(c)
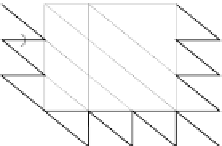
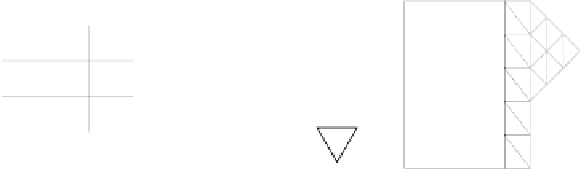
Figure 4.7:
Specifying the 3D shape of a triangulated mesh. (a) We fix the shape of the bottom row
from left to right by rotating each facet with respect to its left neighbor. For each following row, we only
need to set the angle between the leftmost facet and the one below and the angle between the rightmost
facet and its left neighbor. (b) The angles between the facets of the bottom row are first set from left
to right. For each upper row, only the angle of the first facet need be set. (c) Attaching two hexagonal
patches together. Because the base of each triangular patch is attached to the body, only one single angle
is required to fully specify their first row.
the surface, typically yield smooth basis shapes representing low deformation frequencies.This makes
sense because these techniques tend to be employed to create general purpose deformation modes. It
is in contrast to the shape bases used by the NRSFM techniques that will be discussed in Chapter
6
,
which are recomputed for each new sequence and are not restricted to smooth deformations.
Under a linear subspace model, surface deformations are represented as linear combinations
of a relatively small number of basis vectors. This can be expressed as
N
s
x
=
x
0
+
c
i
s
i
=
x
0
+
Sc
,
(4.6)
i
=
1
where
x
is the coordinate vector or Eq.
4.1
, the
s
i
are the basis vectors, and the
c
i
their associated
weights.
S
is a matrix whose columns are the
s
i
and
c
the vector of weights.
In the absence of either a stiffness matrix or sufficient amounts of training data, an approach
to automatically generating deformed shapes was proposed in
Salzmann
et al.
[
2007c
]. It relies on
the fact that the shape of an inextensible triangulated mesh can be parameterized in terms of a
small subset of the angles between its facets, as depicted by Fig.
4.7
. Thus, given a reference shape
represented as a triangulated mesh, a representative set of deformed shapes can be synthesized by
randomly sampling this set of angles and generating the corresponding shapes. The resulting modes,
computed via PCA, were shown to allow reconstructing very general deformable surfaces. In fact, it
was observed that they produced better results than those obtained from a stiffness matrix computed
using a finite element package when the exact physical parameters of the surface were not known and
had to be guessed
Salzmann
[
2009
]. In practice, these modes have been used to reconstruct surfaces
by optimizing their weights so as to minimize an objective function combining information provided
by point correspondences, surface boundaries, and occluding contours. The resulting algorithm was
























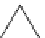

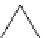






Search WWH ::

Custom Search