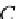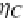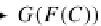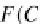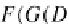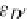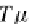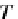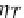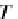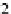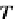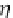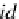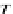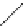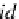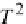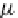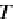Database Reference
In-Depth Information
so that
η
C
is a universal arrow from
C
into
G
and, dually,
ε
D
is a couniversal
arrow from
F
into
D
. Consequently, in an given adjunction, the unit
η
generates a
universal arrow for each object in
C
and counit
ε
generates a couniversal arrow for
each object in
D
. In the case when
C
and
D
are poset categories,
f
and
f
define
this adjunction as a Galois connection, denoted by
F
G
.
Two categories
C
and
D
are
equivalent
if they are adjoint with the unit and counit
whose components are all isomorphisms.
Given an adjunction
(F,G,ε,η)
let us look at the endofunctor
T
=
GF
:
C
→
T
and a natural transformation
C
. We have a natural transformation
η
:
id
C
T
with components for each object
C
,
μ
C
=
T
2
T
2
C
μ
TC
(Here
T
2
denotes the composition
TT
and
T
3
the composition
TTT
). Furthermore,
the equalities (commutative diagrams of natural transformations)
:
G(ε
F(C)
)
:
→
T
3
C
T
3
C
hold. Here
(T μ)
C
=
T(μ
C
)
:
→
TC
and
(μT )
C
=
μ
TC
:
→
TC
(simi-
larly for
ηT
and
Tη
).
Atriple
(T,η,μ)
satisfying these equalities is called a
monad
.
The notion of a monad is one of the most general mathematical notions. For
instance,
every
algebraic theory, that is, every set of operations satisfying equational
laws, can be seen as a monad (which is also a
monoid
in a category of endofunctors
of a given category: the “operation”
μ
being the associative multiplication of this
monoid and
η
its unit).
Thus, monoid laws of the monad do subsume all possible algebraic laws.
We will use monads [
33
,
35
,
36
] for giving
denotational semantics to database
mappings
, and more specifically as a way of modeling computational/collection
types [
8
,
65
,
66
,
68
].
A dual structure to a monad is a comonad
(T,η
C
,μ
C
)
such that all arrows in the
commutative monad's diagrams above are inverted, so that we obtain: