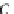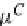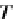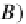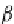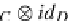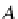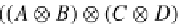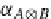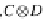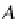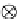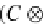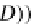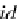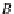Database Reference
In-Depth Information
A
monoidal category
is a structure
(
C
,
⊗
,I,α,β,γ)
where
C
is a category,
⊗:
C
C
is a functor (
tensor
),
I
is a distinguished object of
C
(unit),
α,β,γ
are
natural transformations (
structural isos
for associativity, left and right identity) with
components:
α
A,B,C
:
(A
⊗
B)
⊗
C
A
⊗
(B
⊗
C)
,
β
A
:
I
⊗
A
A
,
γ
A
:
A
⊗
I
A
,
such that the following diagrams commute (coherence conditions)
×
C
→
A
strict
monoidal category is one for which all these natural transformations are
identities.
This very short introduction to category theory is dedicated to experts in DB
theory which did not work previously with the concepts of the category theory.
Chapters
8
and
9
require a more deep expertise in the category theory.
1.5.1 Categorial Symmetry
The concept of categorial symmetry was introduced in my PhD thesis [
44
] with a
number of its applications. Here I will only introduce some of the fundamental prop-
erties of this particular class of categories, which will be considered in the database
category
DB
(one of the principal issues of this manuscript).
It is well known that all categories can be defined by only their morphisms (ar-
rows) because each object is equivalently represented by its identity morphism. Fun-
damentally, a symmetric category has a nice property of a kind of (incomplete) dual-
ity between objects and arrows. In fact, there is an operator '
' for the composition
of objects, analogous to the standard composition of arrows '
∗
◦
'. However, differ-
ently form
◦
that is not commutative (preserves the sequential composition of the