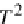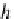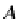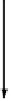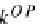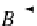Database Reference
In-Depth Information
That is, whenever
m
:
TA
→
B
(with a simple object
B
) has
m
◦
Th
=
m
◦
μ
A
in
DB
, there is exactly one arrow
k
:
A
→
B
such that
m
=
k
◦
h
.Infact,if
m
◦
Th
=
∩
Th
μ
A
and
Th
=
h
we obtain
m
◦
μ
A
then
m
=
m
∩
μ
A
, and from
m
⊆
TA
=
∩
h
⊆
h
. Consequently, in order to satisfy the commutativity
m
m
=
m
, i.e.,
m
=
=
k
∩
h,
we must have that
k
k
◦
h
, that is,
m
=
m
, so that
k
is uniquely determined
by the morphism
m
.
Analogously, we obtain for the equalizer in the right part of the diagram above.
Lemma 16
DB
has the
(
co
)
equalizers for every pair of morphisms
.
B
and hence
f
Proof
For each pair of simple morphisms
f,g
:
A
→
⊆
TA
and
g
⊆
=
(f
∩
g)
∪
(T A
\
(f
∪
g))
⊆
TA
is a limit object (up to isomorphism)
of the diagram
B
TA
,the
LimE
f
g
A
, so that the following diagram is an equalizer:
with (i)
f
m
, where
h
is a monomorphism (every
equalizer is monic). It is easy to verify that
h
◦
h
=
g
◦
h
and (ii)
f
◦
m
=
g
◦
=
T(LimE)
⊆
TA
is the maximal flux
such that
f
∩
h
∩
h
(equal to
f
g
). From (ii) we have
f
=
g
∩
∩
m
=
g
∩
m
,so
⊆
h
and hence for each
m
that it must be
m
:
C
→
A
such that (ii) is true, there is
LimE
with
k
a unique
k
k
. By duality, it is valid for
coequalizers as well. The equalizers for the complex arrows are given as a particular
case of the pullbacks after the proof of next Proposition
48
.
:
C
→
=
m
for which
m
=
h
◦
In the case when
J
is an index category with three objects and two arrows
with the same codomain, each diagram (a functor)
D
∈
DB
J
is of the form
g
B
. The limits of such diagrams are the pullbacks. In the case
when
J
is an index category with one object only, the limit of such diagram cor-
f
C
A